题目内容
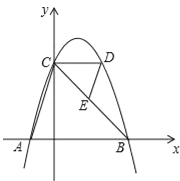
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
【答案】(1)A(﹣1,0),B(3,0);(2)![]() .
.
【解析】
(1)令y=0,即可求A、B的坐标;(2)由CD∥AB,DE∥AC得到△CDE∽△BAC,当y=3时,即可求出D点坐标,得到CD的长,从而得到△CDE与△BAC的相似比,根据相似三角形的面积比等于相似比的平方,得到答案.
(1)∵令y=0,则﹣(x﹣1)2+4=0,解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0);
(2)∵CD∥AB,DE∥AC,
∴△CDE∽△BAC.
∵当y=3时,x1=0,x2=2,∴CD=2.
∵AB=4,∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案为:(1)A(﹣1,0),B(3,0);(2)![]() .
.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目