题目内容
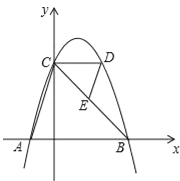
【题目】如图，已知△ABC中，AB＝AC，AD是∠BAC的平分线，AE是∠BAC的外角平分线，ED∥AB交AC于点G，下列结论：①BD＝DC；②AE∥BC；③AE＝AG；④AG＝
DE．正确的是_____（填写序号）
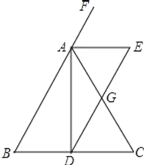
【答案】①②④
【解析】
根据等腰三角形的性质与判定、平行线的性质分别对每一项进行分析判断即可．
解：①∵△ABC中，AB＝AC，AD是∠BAC的平分线，
∴BD＝DC，
故本选项正确，
②∵△ABC中，AB＝AC，AD是∠BAC的平分线，
∴AD⊥BC，
∴AE∥BC，
故本选项正确，
③∵AE∥BC，
∴∠E＝∠EDC，
∵ED∥AB，
∴∠B＝∠EDC，∠AGE＝∠BAC，
∴∠B＝∠E，
∵∠B不一定等于∠BAC，
∴∠E不一定等于∠AGE，
∴AE不一定等于AG，
故本选项错误，
④∵ED∥AB，
∴∠BAD＝∠ADE，
∵∠CAD＝∠BAD，
∴∠CAD＝∠ADE，
∴AG＝DG，
∵AE∥BC，
∴∠EAG＝∠C，
∵∠B＝∠E，∠B＝∠C，
∴∠E＝∠C，
∴∠EAG＝∠E，
∴AG＝EG，
∴AG＝
DE，
故答案为：①②④
练习册系列答案
相关题目
