��Ŀ����
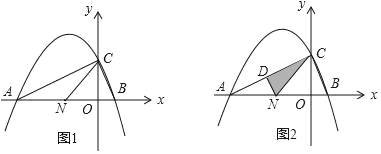
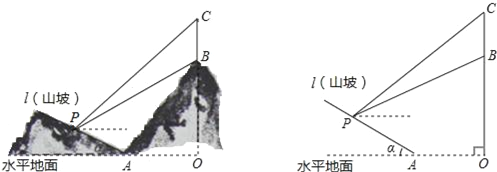
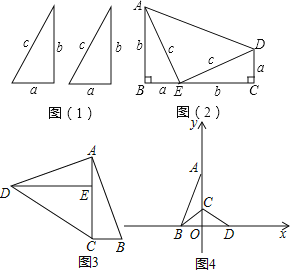
����Ŀ����ͼ��1����������ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc��
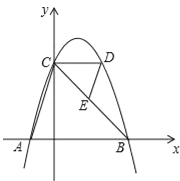
��1�������������������ι������ͼ��2����ͼ�Σ��������ͼ�Σ�֤����a2+b2��c2��
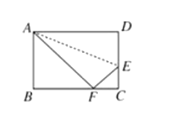
��2�������������������ι���ͼ3��ͼ�Σ������������ͼ��֤�����⣨1���Ľ���������ܣ���д��֤�����̣�
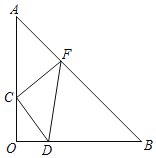
��3����a��3��b��4ʱ��������һ��ֱ�������η���ƽ��ֱ������ϵ�У�ʹֱ�Ƕ�����ԭ���غϣ���ֱ�DZ�a��b�ֱ���x�ᡢy���غϣ���ͼ4��Rt��AOB��λ�ã�����CΪ�߶�OA��һ�㣬����ABC����ֱ��BC���ۣ���Aǡ������x���ϵ�D����
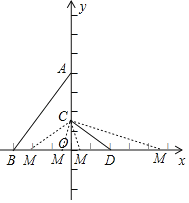
����д��C��D��������ꣻ
������CMDΪ���������Σ���M��x���ϣ���ֱ��д���������������е�M�����꣮
���𰸡���1������������2���ܣ�����������3����C��D���������ΪC��0��![]() ����D��2��0�����ڷ������������е�M������Ϊ����
����D��2��0�����ڷ������������е�M������Ϊ����![]() ��0������
��0������![]() ��0����������2��0��������
��0����������2��0��������![]() ��0��
��0��
��������
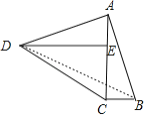
��1���������ε���������ֱ�ʾ��������֤����
��2�������ı���ABCD����������ֱ�ʾ��������֤����
��3���ٸ��ݷ��۵����ʺ��ɶ���������⣻
�ڸ��ݵ��������ε����ʷ����������⼴�ɣ�
�⣺��1����S����ABCD=![]()
S����ABCD=![]()
![]()
![]()
![]() ��
��
��2������![]() ��
��
��ͼ��
S�ı���ABCD=![]() ��
��
S�ı���ABCD=![]() ��
��
![]()
![]() ��
��
![]() ��
��
��3������![]() ����
����![]() ����
����![]() ��
��
���ݷ��ۿ�֪��
![]() ��
��![]() ��
��
![]() ��
��
��![]() �У����ݹ��ɶ�������
�У����ݹ��ɶ�������
![]() ��
��
���![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ���������Ϊ
���������Ϊ![]() ��
��![]() ��
��
����ͼ��
����![]() ��
��![]() ����������ʱ��
����������ʱ��
![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
����![]() ��
��![]() �Ḻ������ʱ��
�Ḻ������ʱ��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��������������е�![]() ������Ϊ��
��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ��
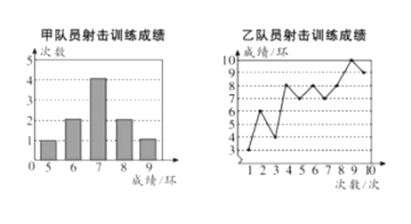
����������Ϣ�����������������£�
ƽ���������� | ��λ�������� | ���������� | ���� | |
�� |
|
|
|
|
�� |
|
|
|
|
��1��������![]() ��
��![]() ��
��![]() ��
��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա�����ѵ���ɼ�����ѡ������һ������������ΪӦѡ������Ա��
��3������������![]() ������
�Σ�����![]() ������ô�ҵ�����ɼ��ķ��� ����������С�����䡱��
������ô�ҵ�����ɼ��ķ��� ����������С�����䡱��