题目内容
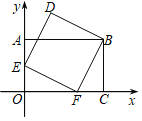
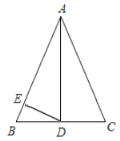
【题目】如图,在不是菱形的平行四边形![]() 中,
中,![]() 在对角线
在对角线![]() 上,在以下三个条件中再选一个,①
上,在以下三个条件中再选一个,①![]() 分别是
分别是![]() 的中线,②
的中线,②![]() 分别是
分别是![]() 的角平分线,③
的角平分线,③![]() .使得四边形
.使得四边形![]() 是平行四边形,并说明理由.
是平行四边形,并说明理由.

【答案】选②能使得四边形![]() 是平行四边形,理由见详解.
是平行四边形,理由见详解.
【解析】
对三个条件进行逐一分析,利用平行四边形的判定方法验证是否能使四边形![]() 是平行四边形,如果能,则可以选择,如果不能,则不能选择.
是平行四边形,如果能,则可以选择,如果不能,则不能选择.
选②能使得四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
∵四边形ABCD是平行四边形,且不是菱形,
∴![]() ,对角线AC不平分对角
,对角线AC不平分对角![]() ,
,
![]() .
.
∵AE平分![]() ,CF平分
,CF平分![]() ,
,
∴![]() ,且AE,CF不在同一直线上.
,且AE,CF不在同一直线上.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,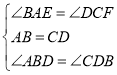
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形AECF是平行四边形;
选择①不能使四边形AECF是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴AC,BD互相平分,
∴若![]() 分别是
分别是![]() 的中线,则AE,CF在同一条直线上,不存在四边形AECF,故不能选①;
的中线,则AE,CF在同一条直线上,不存在四边形AECF,故不能选①;
选③不一定能使四边形AECF是平行四边形,理由是:
∵![]() ,AE与CF不一定平行,
,AE与CF不一定平行,
如图中AE与![]() 相等但不平行,
相等但不平行,
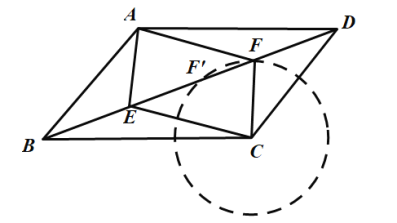
∴四边形AECF不一定是平行四边形,故不能选③.

练习册系列答案
相关题目