题目内容
【题目】已知抛物线y=ax2+ c(a≠0).
(1)若抛物线与x轴交于点B(4,0),且过点P(1,–3),求该抛物线的解析式;
(2)若a>0,c =0,OA、OB是过抛物线顶点的两条互相垂直的直线,与抛物线分别交于A、B 两点,求证:直线AB恒经过定点(0,![]() );
);
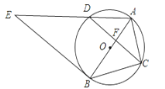
(3)若a>0,c <0,抛物线与x轴交于A,B两点(A在B左边),顶点为C,点P在抛物线上且位于第四象限.直线PA、PB与y轴分别交于M、N两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 为定值,
为定值,![]() =
=![]()
【解析】
(1)把点B(4,0),点P(1,–3)代入y=ax2+ c(a≠0),用待定系数法求解即可;
(2)如图作辅助线AE、BF垂直x轴,设A(m,am2)、B(n,an2),由△AOE∽△OBF,可得到![]() ,然后表示出直线AB的解析式即可得到结论;
,然后表示出直线AB的解析式即可得到结论;
(3)作PQ⊥AB于点Q,设P(m,am2+c)、A(–t,0)、B(t,0),则at2+c=0, c= –at2
由PQ∥ON,可得ON=amt+at2,OM= –amt+at2,然后把ON,OM,OC的值代入整理即可.
(1)把点B(4,0),点P(1,–3)代入y=ax2+ c(a≠0),
![]() ,
,
解之得
 ,
,
∴![]() ;
;
(2)如图作辅助线AE、BF垂直x轴,设A(m,am2)、B(n,an2),

∵OA⊥OB,
∴∠AOE=∠OBF,
∴△AOE∽△OBF,
∴![]() ,
,![]() ,
,![]() ,
,
直线AB过点A(m,am2)、点B(n,an2),
∴![]() 过点(0,
过点(0,![]() );
);
(3)作PQ⊥AB于点Q,设P(m,am2+c)、A(–t,0)、B(t,0),则at2+c=0, c= –at2
∵PQ∥ON,

ON=![]() =
=![]() =
=![]() =
=![]() =at(m+t)= amt+at2,
=at(m+t)= amt+at2,
同理:OM= –amt+at2,
所以,OM+ON= 2at2=–2c=OC,
所以,![]() =
=![]() .
.