题目内容
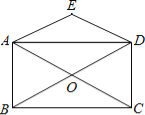
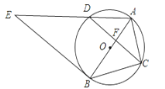
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
【答案】(1)8π;(2)证明见解析.
【解析】
(1)连接OC.设半径为r,在Rt△OFC中利用勾股定理即可解决问题.
(2)只要证明CD∥EB,即可得到∠AFD=∠ABE=90°,由此可以得出结论.
解:(1)连接OC.设半径为r,
∵OA⊥CD,
∴DF=FC=![]() ,
,
在RT△OFC中,∵∠OFC=90°,FC=![]() ,OF=r﹣3,OC=r,
,OF=r﹣3,OC=r,
∴r2=(r﹣3)2+(![]() )2 ,
)2 ,
∴r=4,
∴⊙O的周长为8π.
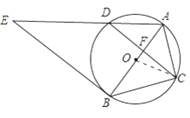
(2)证明:∵OA⊥CD,
∴DF=FC,AD=AC,∠AFD=90°
∴∠ADC=∠ACD,
∵∠E=∠ACD,
∴∠ADC=∠E,
∴CD∥EB,
∴∠AFD=∠ABE=90°,
∴BE是⊙O的切线.

练习册系列答案
相关题目
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.