题目内容
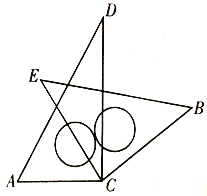
【题目】如图,一艘海轮位于灯塔P的南偏东60方向,距离灯塔100海里的A处,它计划去往位于灯塔P的北偏东45方向上的B处.(参考数据![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险,并说明理由.

【答案】(1)B处距离P有122.5海里(2)没有危险
【解析】试题分析:(1)首先根据题意得出∠MPA=∠PAD=60°,以及∠PDB=∠PBD=45°,再利用解直角三角形求出即可.(2)首先求出OB的长,进而得出OB>50,即可得出答案.
试题解析:
(1)作PC⊥AB于点C
在Rt△PAC中,∠PCA=90,∠CPA=90-60=30
∴PC=PA·cos30=![]()
在Rt△PCB中,∠PCB=90,∠PBC=90-45=45
∴PB=![]() PC=
PC=![]() ≈122.5
≈122.5
∴B处距离P有122.5海里.
(2)没有危险.
理由如下:
OB=OP-PB=![]()
![]() =
=![]()
![]() ,
,
即OB>50,∴无危险

练习册系列答案
相关题目