题目内容
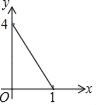
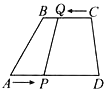
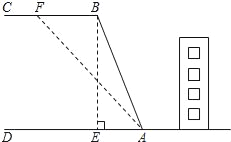
【题目】如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:![]() ,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
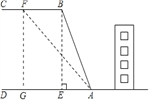
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【答案】(1)改造前坡顶与地面的距离BE为24米;(2)BF至少是8米
【解析】整体分析:
(1)Rt△ABE中,根据斜坡AB的坡比为i=1:![]() ,且AB=26米解直角三角形;(2)过点F作FG⊥AD于点G,用∠FAG的余切求出AG即可.
,且AB=26米解直角三角形;(2)过点F作FG⊥AD于点G,用∠FAG的余切求出AG即可.
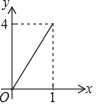
解:(1)在Rt△ABE中,AB=26,i=![]() =
=![]() ,
,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°=![]() =0.75,
=0.75,
∴AG=18,
∴BF=GE=AG﹣AE=8米,
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.