题目内容
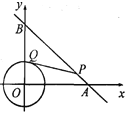
【题目】如图,已知抛物线![]() (b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).


(1)b=______,点B的横坐标为_______(上述结果均用含c的代数式表示);
(2)连结BC,过点A作直线AE//BC,与抛物线交于点E.点D是x轴上一点,坐标为(2,0),当C、D、E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为正整数,则这样的△PBC共有_____个.
【答案】(1)c+![]() ,-2c;(2)y=
,-2c;(2)y=![]() x2-
x2-![]() x-2;(3)①0<S<5;②11.
x-2;(3)①0<S<5;②11.
【解析】
试题分析:本题是二次函数的综合题,其中涉及到运用待定系数法求一次函数、二次函数的解析式,二次函数的性质,直线平移的规律,求两个函数的交点坐标,三角形的面积,一元二次方程的根的判别及根与系数的关系等知识,综合性较强,有一定难度,运用数形结合、分类讨论及方程思想是解题的关键.
(1)将A(-1,0)代入y=![]() x2+bx+c,可以得出b=
x2+bx+c,可以得出b=![]() +c;根据一元二次方程根与系数的关系,得出-1xB=
+c;根据一元二次方程根与系数的关系,得出-1xB=![]() ,即xB=-2c;
,即xB=-2c;
(2)由y=![]() x2+bx+c,求出此抛物线与y轴的交点C的坐标为(0,c),则可设直线BC的解析式为y=kx+c,将B点坐标代入,运用待定系数法求出直线BC的解析式为y=
x2+bx+c,求出此抛物线与y轴的交点C的坐标为(0,c),则可设直线BC的解析式为y=kx+c,将B点坐标代入,运用待定系数法求出直线BC的解析式为y=![]() x+c;由AE∥BC,设直线AE得到解析式为y=
x+c;由AE∥BC,设直线AE得到解析式为y=![]() x+m,将点A的坐标代入,运用待定系数法求出直线AE得到解析式为y=
x+m,将点A的坐标代入,运用待定系数法求出直线AE得到解析式为y=![]() x+
x+![]() ;解方程组
;解方程组 ,求出点E坐标为(1-2c,1-c),将点E坐标代入直线CD的解析式y=-
,求出点E坐标为(1-2c,1-c),将点E坐标代入直线CD的解析式y=-![]() x+c,求出c=-2,进而得到抛物线的解析式为y=
x+c,求出c=-2,进而得到抛物线的解析式为y=![]() x2-
x2-![]() x-2;
x-2;
(3)①分两种情况进行讨论:(Ⅰ)当-1<x<0时,由0<S<S△ACB,易求0<S<5;(Ⅱ)当0<x<4时,过点P作PG⊥x轴于点G,交CB于点F.设点P坐标为(x,![]() x2-
x2-![]() x-2),则点F坐标为(x,
x-2),则点F坐标为(x,![]() x-2),PF=PG-GF=-
x-2),PF=PG-GF=-![]() x2+2x,S=
x2+2x,S=![]() PFOB=-x2+4x=-(x-2)2+4,根据二次函数的性质求出S最大值=4,即0<S≤4,则0<S<5;
PFOB=-x2+4x=-(x-2)2+4,根据二次函数的性质求出S最大值=4,即0<S≤4,则0<S<5;
②由0<S<5,S为整数,得出S=1,2,3,4.分两种情况进行讨论:(Ⅰ)当-1<x<0时,根据△PBC中BC边上的高h小于△ABC中BC边上的高AC=![]() ,得出满足条件的△PBC共有4个;(Ⅱ)当0<x<4时,由于S=-x2+4x,根据一元二次方程根的判别式,得出满足条件的△PBC共有7个;则满足条件的△PBC共有4+7=11个.
,得出满足条件的△PBC共有4个;(Ⅱ)当0<x<4时,由于S=-x2+4x,根据一元二次方程根的判别式,得出满足条件的△PBC共有7个;则满足条件的△PBC共有4+7=11个.
试题解析:(1)b=c+![]() ,点B的横坐标为-2c.
,点B的横坐标为-2c.
(2)由y=![]() x2+(c+
x2+(c+![]() )x+c=
)x+c=![]() (x+1)(x+2c),设E(x,
(x+1)(x+2c),设E(x,![]() (x+1)(x+2c)).
(x+1)(x+2c)).
如图1,过点E作EH⊥x轴于H.
由于OB=2OC,当AE//BC时,AH=2EH.
所以x+1=(x+1)(x+2c).因此x=1-2c.所以E(1-2c,1-c).
当C、D、E三点在同一直线上时,![]() .所以
.所以![]() =
=![]() .
.
整理,得2c2+3c-2=0.解得c=-2或c=![]() (舍去).
(舍去).
所以抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
(3)①当P在BC下方时,过点P作x轴的垂线交BC于F,如图2.
直线BC的解析式为y=![]() x-2.
x-2.
设P(m,![]() m2-
m2-![]() m-2),那么P(m,
m-2),那么P(m,![]() m-2),FP=-
m-2),FP=-![]() m2+2m.
m2+2m.
所以S△PBC=S△PBF+S△PCF=![]() FP(xB-xC)=2FP=-m2+4m=-(m-2)2+4.
FP(xB-xC)=2FP=-m2+4m=-(m-2)2+4.
因此当P在BC下方时,△PBC的最大值为4.
当P在BC上方时,因为S△ABC=5,所以S△PBC<5.
综上所述,0<S<5.
②若△PBC的面积S为正整数,则这样的△PBC共有11个.


 口算能手系列答案
口算能手系列答案