题目内容
【题目】（本小题满分10分）
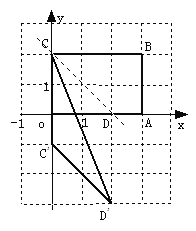
如图，长方形OABC中，O为平面直角坐标系的原点，点A、C的坐标分别为A（3，0）、
C（0，2），点B在第一象限。
(1)写出点B的坐标；
(2)若过点C的直线交长方形的OA边于点D，且把长方形OABC的周长分成2∶3的两部分，求点D的坐标；
(3)如果将（2）中的线段CD向下平移3个单位长度，得到对应线段C′D′，在平面直角坐标系中画出△CD′C′，并求出它的面积。
【答案】（1）B（3，2） ………………………2分
（2）长方形OABC的周长为10. …………………3分
点D在OA边上，把长方形OABC的周长分成2 ：3两部分。∵OC+OA=5<6 ∴只能OC+OD=4
又∵OC=2
∴OD=4-2=2
D(2，0) …………………5分
（3）三角形C D
C如图 ………………………7分
CC=3 D(2，-3) ……………………………8分
三角形C DC的面积为：
………………10分
【解析】略
练习册系列答案
相关题目
