题目内容
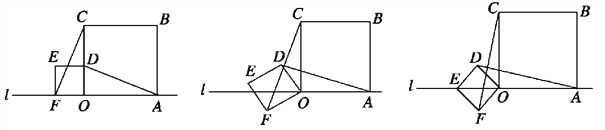
【题目】小明在数学活动课上,将边长为![]() 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
![]()
【答案】解:(1)AD=CF。理由如下:
在正方形ABCO和正方形ODEF中,∵AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF。
在△AOD和△COF中,∵AO=CO,∠AOD=∠COF,OD=OF,
∴△AOD≌△COF(SAS)。
∴AD=CF。
(2)与(1)同理求出CF=AD,

如图,连接DF交OE于G,则DF⊥OE,DG=OG=![]() OE,
OE,
∵正方形ODEF的边长为![]() ,∴OE=
,∴OE=![]() ×
×![]() =2。
=2。
∴DG=OG=![]() OE=
OE=![]() ×2=1。
×2=1。
∴AG=AO+OG=3+1=4,
在Rt△ADG中, ![]() ,
,
∴CF=AD=![]() 。
。
【解析】(1)根据正方形的性质可得AO=CO,OD=OF,∠AOC=∠DOF=90°,然后求出∠AOD=∠COF,再利用“边角边”证明△AOD和△COF全等,根据全等三角形对应边相等即可得证。
(2)与(1)同理求出CF=AD,连接DF交OE于G,根据正方形的对角线互相垂直平分可得DF⊥OE,DG=OG![]() OE,再求出AG,然后利用勾股定理列式计算即可求出AD。
OE,再求出AG,然后利用勾股定理列式计算即可求出AD。

练习册系列答案
相关题目

