题目内容
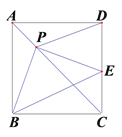
【题目】如图,△ABC中AB=AC,∠A=36°,BD、CE为角平分线,交于O,则图中等腰三角形共有( )

A. 6个 B. 7个 C. 8个 D. 9个
【答案】C
【解析】∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=![]() ,
,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴△ABC,△ABD,△ACE,△BFC是等腰三角形,
∵∠BEC=180°∠ABC∠BCE=72°,∠CDB=180°∠BCD∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BF,CF=CD,BC=BD=CF,
∴△BEF,△CDF,△BCD,△CBE是等腰三角形。
∴图中的等腰三角形有8个。
故选C.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目