题目内容
【题目】如图,点P是反比例函数y= ![]() (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
(k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ![]() .
.
(1)k的值是;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .
【答案】
(1)-4
(2)0<a<2或 ![]() <a<
<a< ![]()
【解析】解:(1.)如图,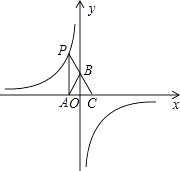
PA垂直x轴于点A(﹣1,0),
∴OA=1,可设P(﹣1,t).
又∵AB= ![]() ,
,
∴OB= ![]() =
= ![]() =2,
=2,
∴B(0,2).
又∵点C的坐标为(1,0),
∴直线BC的解析式是:y=﹣2x+2.
∵点P在直线BC上,
∴t=2+2=4
∴点P的坐标是(﹣1,4),
∴k=﹣4.
所以答案是:﹣4;
解法二:用相似三角形
由题意易得△CPA~CBO,
∴ ![]()
∴ ![]()
∴AP=4,
∴k=﹣4.
(2.)分类讨论
①如图1,延长线段BC交双曲线于点M.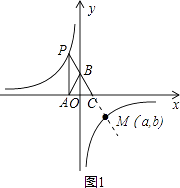
由(1)知,直线BC的解析式是y=﹣2x+2,反比例函数的解析式是y=﹣ ![]() .
.
则 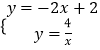 ,
,
解得, ![]() 或
或 ![]() (不合题意,舍去).
(不合题意,舍去).
根据图示知,当0<a<2时,∠MBA<∠ABC;
②如图,作C关于直线AB的对称点C′,连接BC′并延长交双曲线于点M′.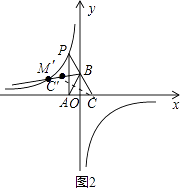
∵A(﹣1,0),B(0,2),
∴直线AB的解析式为:y=2x+2.
直线CC′是与直线AB垂直的,
根据两条直线垂直,两直线的斜率互为负倒数,即:k1k2=﹣1
可设CC′解析式为:y=﹣ ![]() x+b,
x+b,
∵C(1,0),
∴b= ![]() ,
,
∴CC′解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
∵AC=AC′=2,
∴设C′点横坐标为:x,则纵坐标为:﹣ ![]() x+
x+ ![]() ,
,
∴(﹣x﹣AO)2+(﹣ ![]() x+
x+ ![]() )2=(AC′)2 ,
)2=(AC′)2 ,
解得:x1=﹣ ![]() ,x2=1(不合题意舍去),
,x2=1(不合题意舍去),
∴C′(﹣ ![]() ,
, ![]() ),则易求直线BC′的解析式为:y=
),则易求直线BC′的解析式为:y= ![]() x+2,
x+2,
∴ 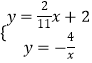 ,
,
解得:x1= ![]() ,x2=
,x2= ![]() ,
,
则根据图示知,当 ![]() <a<
<a< ![]() 时,∠MBA<∠ABC.
时,∠MBA<∠ABC.
综合①②知,当0<a<2或 ![]() <a<
<a< ![]() 时,∠MBA<∠ABC.
时,∠MBA<∠ABC.
故答案是:0<a<2或 ![]() <a<
<a< ![]() .
.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.