题目内容
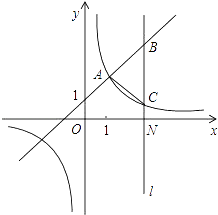
【题目】在平面直角坐标系xOy中，点P是抛物线：y=x2上的动点（点在第一象限内）．连接 OP，过点0作OP的垂线交抛物线于另一点Q．连接PQ，交y轴于点M．作PA丄x轴于点A，QB丄x轴于点B．设点P的横坐标为m．
（1）如图1，当m= 
时，
①求线段OP的长和tan∠POM的值；
②在y轴上找一点C，使△OCQ是以OQ为腰的等腰三角形，求点C的坐标；
（2）如图2，连接AM、BM，分别与OP、OQ相交于点D、E．
①用含m的代数式表示点Q的坐标；
②求证：四边形ODME是矩形．
【答案】
（1）
解：①∵把x= 
代入 y=x2，得 y=2，
∴P（ ，2），
∴OP= 
∵PA丄x轴，
∴PA∥MO．
∴tan∠P0M=tan∠0PA= 
= 
．
②设 Q（n，n2），
∵tan∠QOB=tan∠POM，
∴ 
．
∴n=-
∴Q（- ， 
），
∴OQ= 
．
当OQ=OC时，则C1（0， ），C2（0，- ）；
当OQ=CQ时，则C3（0，1）；
当CQ=CO时，OQ为底，不合题意．
综上所述，当△OCQ是以OQ为腰的等腰三角形时，所求点C坐标为：C1（0， ），C2（0，- ），C3（0，1）
（2）
解：方法一：
①设 Q（n，n2），
∵△APO∽△BOQ，
∴ 
∴ 
，得n=- 
，
∴Q（- ， 
）．
②设直线PQ的解析式为：y=kx+b，把P（m，m2）、Q（- ， ）代入，得：
，
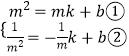①﹣②得：m2﹣ =（m+ ）k，
解得：k=m﹣ ③，
把③代入①，得：b=1，
∴M（0，1）
∵ 
，∠QBO=∠MOA=90°，
∴△QBO∽△MOA
∴∠MAO=∠QOB，
∴QO∥MA
同理可证：EM∥OD
又∵∠EOD=90°，
∴四边形ODME是矩形．
方法二：
①OP⊥OQ，∴KOP×KOQ=﹣1，
∵KOP= 
= ，KOQ=﹣ ，
∴lOQ：y=﹣ x，y=x2
∴x1=0（舍），x2=﹣ ，
∴Q（﹣ ， ），
设点C（0，t），O（0，0），
∵△OCQ是以OQ为腰的等腰三角形．
∴OQ=OC或QO=QC，
∴（0+ ）2+（0﹣ ）2=（0﹣0）2+（0﹣t）2，∴t=± ，
∴（0+ ）2+（0﹣ ）2=（﹣ ﹣0）2+（ ﹣t）2，∴t=1，
∴C1（0， ），C2（0，﹣ ），C3（0，1），
∵Px=m，∴PY=m2，∴KOP=m，
又OQ⊥OP，∴KOP×KOQ=﹣1，∴KOQ=﹣ ，
∴lOQ：y=﹣ x，
∵y=x2，
∴Q（﹣ ， ），P（m，m2），
∴lPQ：y=（m﹣ ）x+1，
即M（0，1），又A（m，0），B（﹣ ，0），O（0，0），
∴KAM= 
=﹣ ，∵KOQ=﹣ ，KAM=KOQ，∴AM∥OQ，
∴KBM= 
=m，∵KOP=m，∴KBM=KOP，∴BM∥OP，
∴四边形ODME是平行四边形，又OP⊥OQ，
∴四边形ODME为矩形．
【解析】方法一：（1）①已知m的值，代入抛物线的解析式中可求出点P的坐标；由此确定PA、OA的长，通过解直角三角形易得出结论．②题干要求△OCQ是以OQ为腰的等腰三角形，所以分QO=OC、QC=QO、CQ=CO三种情况来判断：QO=QC时，Q在线段OC的垂直平分线上，Q、O的纵坐标已知，C点坐标即可确定；QO=OC时，先求出OQ的长，那么C点坐标可确定；
CQ=CO时，OQ为底，不合题意．（2）①由∠QOP=90°，易求得△QBO∽△MOA，通过相关的比例线段来表示出点Q的坐标；②在四边形ODME中，已知了一个直角，只需判定该四边形是平行四边形即可，那么可通过证明两组对边平行来得证．方法二：（1）略．（2）利用黄金法则二求出直线OQ的斜率与抛物线联立求出Q点坐标，再利用黄金法则四求出C点坐标3分别求出点M，A，O，B坐标，利用斜率相等，证明MA‖OQ，BM‖OP，从而得出四边形ODME是平行四边形，再利用OP⊥OQ证明矩形．
