��Ŀ����
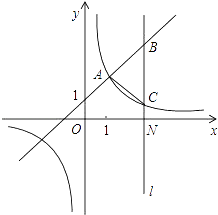
����Ŀ����ͼ1����A��x���������ϵĶ��㣬��B����Ϊ��0��4����M���߶�AB���е㣬����M�Ƶ�A˳ʱ�뷽����ת90��õ���C������C��x��Ĵ��ߣ�����ΪF������B��y��Ĵ�����ֱ��CF�ཻ�ڵ�E����D�ǵ�A����ֱ��CF�ĶԳƵ㣬����AC��BC��CD�����A�ĺ�����Ϊt��
��1����t=2ʱ����CF�ij���
��2���ٵ�tΪ��ֵʱ����C�����߶�BD�ϣ�
�����BCE�����ΪS����S��t֮��ĺ�����ϵʽ��
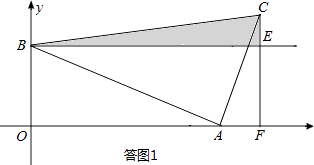
��3����ͼ2������C���E�غ�ʱ������CDF��x������ƽ�Ƶõ���C��D��F�䣬�ٽ�A��B��C�䣬D��Ϊ������ı�����C��F��������õ�����ͼ�Σ���������ͼ��ƴ�ɲ��ص�����϶��ͼ��ǡ���������Σ���ֱ��д�����з������������ĵ�C������꣮
���𰸡�
��1��
�⣺�����⣬��֤Rt��ACF��Rt��BAO��
�� ![]() ��
��
��AB=2AM=2AC��
��CF= ![]() OA=
OA= ![]() t��
t��
��t=2ʱ��CF=1
��2��
�⣺���ɣ�1��֪��Rt��ACF��Rt��BAO��
�� ![]() ��
��
��AF= ![]() OB=2��
OB=2��
��FD=AF=2����
�ߵ�C�����߶�BD�ϣ�
���DCF�ס�DBO��
�� ![]() ����
���� ![]() ��
��
���t= ![]() ��2��t=��
��2��t=�� ![]() ��2��С��0����ȥ��
��2��С��0����ȥ��
�൱t= ![]() ��2ʱ����C�����߶�BD�ϣ�
��2ʱ����C�����߶�BD�ϣ�
�ڵ�0��t��8ʱ������ͼ1��ʾ��
S= ![]() BECE=
BECE= ![]() ��t+2����4��
��t+2����4�� ![]() t��=-
t��=- ![]() t2+
t2+ ![]() t+4��
t+4��
��t��8ʱ�����ͼ1��ʾ��
S= ![]() BECE=
BECE= ![]() ��t+2����
��t+2���� ![]() t��4��=
t��4��= ![]() t2��
t2�� ![]() t��4
t��4
��3��
�⣺���������ĵ�C������Ϊ����12��4������8��4����2��4����
�������£�
�ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣�
����һ�����ͼ2��ʾ����F��C��=AF��ʱ����F�������Ϊ��12��0����
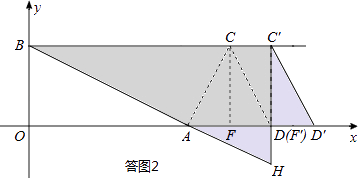
���ݡ�C��D��F��ա�AHF�䣬��BC��HΪƴ�ɵ������Σ���ʱC�������Ϊ��12��4����
�����������ͼ3��ʾ������F�����A�غ�ʱ����F�������Ϊ��8��0����

���ݡ�OC��A�ա�BAC�䣬��֪��OC��D��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��8��4����
����������BC��=F��D��ʱ����F�������Ϊ��2��0����
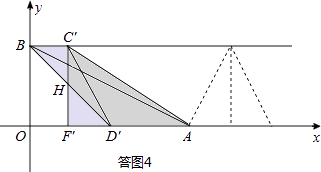
���ݡ�BC��H�ա�D��F��H����֪��AF��C��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��2��4��
����������1����Rt��ACF��Rt��BAO����CF= ![]() OA=
OA= ![]() t���ɴ����CF��ֵ����2������Rt��ACF��Rt��BAO���������AF�ij��ȣ�����C�����߶�BD�ϣ����С�DCF�ס�DBO���������Ʊ���ʽ�з������t��ֵ��
t���ɴ����CF��ֵ����2������Rt��ACF��Rt��BAO���������AF�ij��ȣ�����C�����߶�BD�ϣ����С�DCF�ס�DBO���������Ʊ���ʽ�з������t��ֵ��
���������������Ҫ�������ۣ���0��t��8ʱ������ͼ1��ʾ����t��8ʱ�����ͼ1��ʾ����3�������漰ͼ�εļ�ƴ���ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣���Ҫ�������ۣ��ֱ����ͼ2��4��ʾ��
�����㾫����������Ҫ����������ͼ�κ����������ε��ж������ʵ����֪ʶ�㣬��Ҫ������״��ͬ����С��һ����ͬ���Ŵ����С��;�ж�:��ƽ�У���������ȣ������߶�Ӧ�ɱ������н���ȣ������߶�Ӧ�ɱ��������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��������ȷ�����⣮

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�