��Ŀ����
����Ŀ����ͼ��ƽ���ı���ABCD�������16���Խ���AC��BD�ཻ�ڵ�O����M1��N1��P1�ֱ�Ϊ�߶�OD��DC��CO���е㣬˳������M1N1��N1 P1��P1M1�õ���һ����P1M1N1 �� ���ΪS1 �� �ֱ�ȡM1N1��N1P1��P1M1���ߵ��е�P2��M2��N2 �� �õ��ڶ�����P2M2N2 �� �����ΪS2 �� ��˼�����ȥ�õ���n����PnMnNn �� �����ΪSn �� ��Sn��Sn��1= �� ���ú�n�Ĵ���ʽ��ʾ��n��2��nΪ������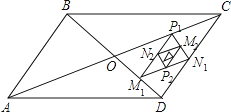
���𰸡�![]()
���������⣺��ƽ���ı���ABCD���Խ������ֵ��ĸ�С�����������ȣ���S��OCD=16�� ![]() =4��
=4��
��M1��N1��P1�ֱ�Ϊ�����е㣬�ʽ���OCD��Ϊ�ĸ������ȵ������Σ�
��S��M1N1P1=4�� ![]() =1���������£�M2��N2��P2�ֽ���M1N1P1�������Ϊ����ķ֣���S2=S��M2N2P2=
=1���������£�M2��N2��P2�ֽ���M1N1P1�������Ϊ����ķ֣���S2=S��M2N2P2= ![]() S��M1N1P1=4��
S��M1N1P1=4�� ![]() ��
�� ![]() =4��
=4�� ![]() ��
��
�������ơ�
��Sn=4�� ![]() ����Sn��1=4��
����Sn��1=4�� ![]() ����Sn��Sn��1=4��
����Sn��Sn��1=4�� ![]() ��4��
��4�� ![]() =��
=�� ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫����������Ĺؼ�����������������λ�߶��������֪ʶ���������������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룬�Լ���ƽ���ı��ε����ʵ����⣬�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�