��Ŀ����
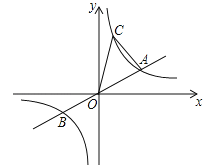
����Ŀ����ͼ�������ߵĶԳ�����ֱ��x=2������A��������Ϊ1����B��4��0���ڴ��������ϣ�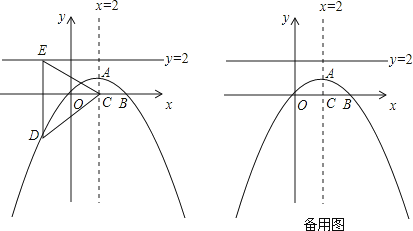
��1����������ߵĽ���ʽ��
��2�����������߶Գ�����x�ύ��ΪC����D��x��y��Ϊ��������һ���㣬����D��ֱ��y=2�Ĵ��ߣ�����ΪE��
���ú�y�Ĵ���ʽ��ʾCD2 �� ������CD2��DE2֮���������ϵ�������֤����
���ڴ����������Ƿ���ڵ�D��ʹ��EDC=120�㣿������ڣ���ֱ��д��D�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�����⣬�������ߵĽ���ʽΪ��y=a��x��2��2+1������B��4��0�����ã�
a��4��2��2+1=0����ã�a=�� ![]()
�������ߵĽ���ʽ��y=�� ![]() ��x��2��2+1
��x��2��2+1
��2��
�⣺
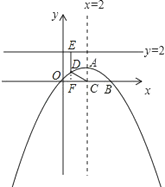
�ٲ��룺CD2=DE2��
֤������D��x��y����C��2��0����E��x��2��֪��
CD2=��x��2��2+y2��DE2=��y��2��2��
�ɣ�1��֪����x��2��2=��4��y��1��=��4y+4������CD2�У��ã�
CD2=y2��4y+4=��y��2��2=DE2��
�����ڡ�EDC=120�㣾90�㣬���Ե�D����x���Ϸ����������߶Գ��������������һ���������Ϊ����
�ӳ�ED��x����F����EF��x�
��Rt��CDF�У���FDC=180�㩁120��=60�㣬��DCF=30�㣬��
CD=2DF��CF= ![]() DF��
DF��
��DF=m����CF= ![]() m��CD=DE=2m��
m��CD=DE=2m��
��EF=ED+DF=2m+m=2��
��m= ![]() ��DF=m=
��DF=m= ![]() ��CF=
��CF= ![]() m=
m= ![]() ��OF=OC��CF=2��
��OF=OC��CF=2�� ![]() ��
��
��D��2�� ![]() ��
�� ![]() ����
����
ͬ���������߶Գ����Ҳ��У�D��2+ ![]() ��
�� ![]() ����
����
���ϣ����ڷ���������D�㣬������Ϊ��2�� ![]() ��
�� ![]() ����2+
����2+ ![]() ��
�� ![]() ����
����
����������1����֪�����ߵĶ������꣬���Խ������ߵĽ���ʽ��Ϊ����ʽ���ٴ���B���������⼴�ɣ���2����������ϵ�����ľ��빫ʽ���ѵõ�CD2��DE2�ı���ʽ���ٽ���1���������߽���ʽ����CD2�ı���ʽ�У���y�滻��x�Ƚ����ߵĴ�С��ϵ���ɣ��ڡ�EDC�Ƕ۽ǣ���ô��Dһ����x����Ϸ����������߶Գ�������������һ�������ǹ��������߶Գ���Գƣ����ӳ�ED��x����F����Rt��CDF�У���DCF=30�㣬��ôDC=2DF��CF= ![]() DF�����DF�ij����Ա�ʾ��CD��DE�ij�����EF=ED+DF=2���ɵó�DF�ij����Ӷ������D�����꣮
DF�����DF�ij����Ա�ʾ��CD��DE�ij�����EF=ED+DF=2���ɵó�DF�ij����Ӷ������D�����꣮