题目内容
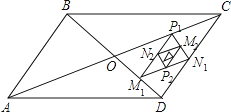
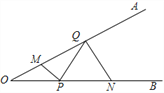
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
【答案】![]()
【解析】试题分析:本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.
解:作M关于OB的对称点M′,作N关于OA的对称点N′,
连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′=![]() =
=![]() .
.
故答案为![]() .
.


练习册系列答案
相关题目