题目内容
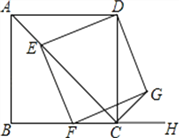
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)见解析;(2) 是定值
【解析】分析:①作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;
②同①的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.
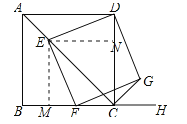
详解:①过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°, 且NE=NC,∴四边形EMCN为正方形.
∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,又∠DNE=∠FME=90°.在△DEN和△FEM中,∵∠DNE=∠FME,EN=EM,∠DEN=∠FEM,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,
②CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°.
∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG.在△ADE和△CDG中,∵AD=CD,∠ADE=∠CDG,DE=DG,∴△ADE≌△CDG(SAS),∴AE=CG,
∴AC=AE+CE=![]() AB=
AB=![]() ×2
×2![]() =4,∴CE+CG=4 是定值.
=4,∴CE+CG=4 是定值.

练习册系列答案
相关题目