题目内容
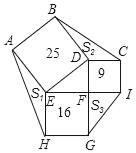
【题目】如图,![]() 是等腰直角
是等腰直角![]() 外一点,把
外一点,把![]() 绕直角顶点
绕直角顶点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 的值为________.
的值为________.

【答案】1:2
【解析】
如图,连接AP,构建全等三角形:△ABP≌△CBP′(SAS),由该全等三角形的对应边相等得到AP=P′C;如图,连接PP′,结合已知条件可以推知△APP′是直角三角形,所以由勾股定理来求相关线段的长度即可.
如图,连接AP,

∵BP绕点B顺时针旋转![]() 到BP′,
到BP′,
∴BP=BP′,∠ABP+∠ABP′=![]() ,
,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=![]() ,
,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
∵
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
连接PP′,则△PBP′是等腰直角三角形,
∴![]()
∵![]()
∴![]()
∴△APP′是直角三角形,
设P′A=x,则AP=3x,
根据勾股定理,![]()
∴![]()
解得PB=2x,
∴P′A:PB=x:2x=1:2.
故答案为:1:2.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】若a,b是一元二次方程x(x﹣2)=x﹣2的两根,且点A(﹣a,﹣b)是反比例函数图象上的一个点,若自点A向两坐标轴作垂线,两垂线与坐标轴构成的矩形的面积是( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
【题目】元旦期间,为了满足颍上县百姓的消费需要,某大型商场计划用170000元购进一批家电,这批家里的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商场购买冰箱x台.
(1)用含x的代数式表示洗衣机的台数.
(2)商场至多可以购买冰箱多少台?
(3)购买冰箱多少台时,能使商场销售完这批家电后获得的利润最大?最大利润为多少元?
【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分) | |
八年1班 | 80 86 88 80 88 99 80 74 91 89 |
八年2班 | 85 85 87 97 85 76 88 77 87 88 |
八年3班 | 82 80 78 78 81 96 97 87 92 84 |
解答下列问题:
(1)请填写下表:
平均数(分) | 众数(分) | 中位数(分) | |
八年1班 | 85.5 |
| 87 |
八年2班 | 85.5 | 85 |
|
八年3班 |
| 78 | 83 |
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.