��Ŀ����
����Ŀ����֪���ס��������ֱ�����300km��A,B����ͬʱ����������У���B�غ��������أ���ͼ����������Գ����صľ���y����ʻʱ��x֮��ĺ���ͼ��.
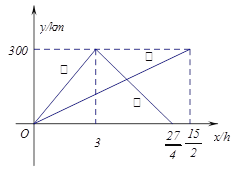
��1����׳�������صľ���y����ʻʱ��x֮��ĺ�����ϵʽ���������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������֪�ҳ���ʻ���ٶ���40ǧ��/Сʱ���������ʱ�䣬��������Գ����صľ�����ȣ�
��3����������ʻ�������м�������.�����ÿ��������ʱ��.
���𰸡�(1) 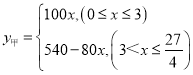 ;(2)4.5Сʱ;(3) :�����״�������
;(2)4.5Сʱ;(3) :�����״�������![]() h,�ڶ���������6h.
h,�ڶ���������6h.
��������
(1)�������ʽ,�ֶ����۴�ֵ�������.
(2)��ͼ�ó��ҳ���Ӧ��һ�κ�����׳�һ�κ����������������.
(3)��ͼ��֪��������������,�ֱ����ۼ��㼴��.
(1)��0��x��3ʱ,������������,��Ϊy=kx,
��x=3ʱ,y=300,������k=100,����y=100x��
��3��x��![]() ʱ,��һ�κ���,��Ϊy=kx+b,
ʱ,��һ�κ���,��Ϊy=kx+b,
�������㣨3,300������![]() ,0��,���k=-80,b=540,����y=540-80x ��
,0��,���k=-80,b=540,����y=540-80x ��
�ۺ����ϵü׳�������صľ���y����ʻʱ��x֮��ĺ�����ϵʽ
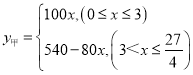
(2)�������:y��=40x����0��x��![]() ��
��
��40x=100xʱ,����ȥ
��40x=540-80xʱ,���x=4.5
������4.5Сʱ,��������Գ����صľ������.
(3)��ͼ��ɵ�����������.
�辭��aСʱ�����״�����,��40a+100a=300,���a=![]() ,
,
�辭��bСʱ�����ڶ�������,��80��b-3��=40b,���b=6��
��:�����״�������![]() h,�ڶ���������6h.
h,�ڶ���������6h.

 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�




