Question

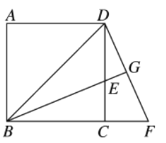
【题目】如图，BD是边长为1的正方形ABCD的对角线，BE平分∠DBC交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G.

（1）求证：△BCE≌△DCF；

（2）求CF的长。

Answer 1

【答案】（1）证明见解析；（2）-1.

【解析】

（1）利用正方形的性质，由全等三角形的判定定理SAS，即可证得△BCE≌△DCF；

（2）由BE平分∠DBC，BD是正方形ABCD的对角线，及△BCE≌△DCF可得∠DEG=∠BEC，∠BGD=∠BCD=90°=∠BGF.从而得到△DBG≌△FBG，根据全等三角形的性质可得BF的长，最后由勾股定理及线段的和差，即可求得CF的长度.

（1）∵四边形ABCD为正方形，

∴CB=CD，∠BCD=90°，

∴∠DCF=180°-∠BCD=90°，

在△BCE和△DCF中，

，

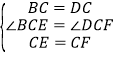∴△BCE≌△DCF；

（2）∵BD是正方形ABCD的对角线，

∠DBC=∠ABC==45°，

∵BE平分∠DBC，

∴∠EBC=∠DBC=22.5°，

由（1）知△BCE≌△DCF，

∴∠EBC=∠FDC=22.5°，

∵∠DEG=∠BEC，

∴∠BGD=∠BCD=90°=∠BGF，

在△DBG和△FBG中，

，

∴△DBG≌△FBG，

∴BD=BF，DG=FG，

∵BD=，

∴BF=，

∴CF=BF-BC=-1.