��Ŀ����
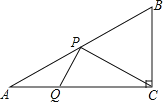
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��40cm����A��60�㣬��D�ӵ�C������CA������4cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��10��������D��DF��BC�ڵ�F������DE��EF��
��1���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��2����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
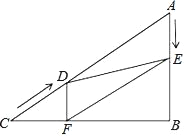
���𰸡���1���ܣ���t��![]() ��ʱ���ı���AEFDΪ���Σ�����������2����t��8��5��ʱ����DEFΪֱ�������Σ�������.
��ʱ���ı���AEFDΪ���Σ�����������2����t��8��5��ʱ����DEFΪֱ�������Σ�������.
��������
��1���ܣ�����֤���ı���AEFDΪƽ���ı��Σ���AE��ADʱ���ı���AEFDΪ���Σ���40��4t��2t���ⷽ�̼��ɽ�����⣻
��2���������������ۼ��ɣ�
��1��֤�����ܣ�
�������£�����DFC�У���DFC��90������C��30����DC��4t��
��DF��2t��
�֡�AE��2t��
��AE��DF��
��AB��BC��DF��BC��
��AE��DF��
�֡�AE��DF��
���ı���AEFDΪƽ���ı��Σ�
��AE��ADʱ���ı���AEFDΪ���Σ�
��40��4t��2t�����t��![]() ��
��
�൱t��![]() ��ʱ���ı���AEFDΪ���Σ�
��ʱ���ı���AEFDΪ���Σ�
��2���ٵ���DEF��90��ʱ���ɣ�1��֪�ı���AEFDΪƽ���ı��Σ�
��EF��AD��
���ADE����DEF��90����
�ߡ�A��60����
���AED��30����
��AD��![]() AE��t��
AE��t��
��AD��40��4t����40��4t��t�����t��8��
�ڵ���EDF��90��ʱ���ı���EBFDΪ���Σ���Rt��AED�С�A��60�������ADE��30����
��AD��2AE����40��4t��4t�����t��5��
������EFD��90������E��B�غϣ�D��A�غϣ�������������ڣ�
������������t��8��5��ʱ����DEFΪֱ�������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�