Question

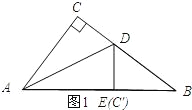
【题目】如图，在Rt△ABC中，∠ACB=90°,AB=5,AC=3,点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点C'处，连接C'D交AB于点E，连接BC'，当△BC'D是直角三角形时，DE的长为_________.

Answer 1

【答案】或

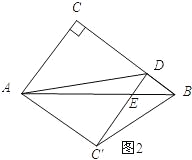
【解析】试题分析：如图1所示；点E与点C′重合时．在Rt△ABC中，BC==4．由翻折的性质可知；AE=AC=3、DC=DE．则EB=2．设DC=ED=x，则BD=4﹣x．在Rt△DBE中，DE2+BE2=DB2，即x2+22=（4﹣x）2．解得：x=．∴DE=．如图2所示：∠EDB=90时．由翻折的性质可知：AC=AC′，∠C=∠C′=90°．∵∠C=∠C′=∠CDC′=90°，∴四边形ACDC′为矩形．又∵AC=AC′，∴四边形ACDC′为正方形．∴CD=AC=3．∴DB=BC﹣DC=4﹣3=1．∵DE∥AC，∴△BDE∽△BCA．∴，即．解得：DE=．点D在CB上运动，∠DBC′＜90°，故∠DBC′不可能为直角．