题目内容
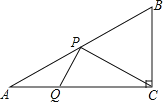
【题目】在Rt△ABC中,∠BAC=30°,斜边AB=2![]() ,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值=__________ .
,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值=__________ .
【答案】2
【解析】
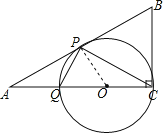
以CQ为直径作⊙O,当⊙O与AB边相切动点P时,CQ最短,根据切线的性质求得OP⊥AB,进而根据已知求得△POQ为等边三角形,得出∠APQ=30°,设PQ=OQ=OP=OC=r,3r=AC=cos30°AB=![]() =3,从而求得CQ的最小值为2.
=3,从而求得CQ的最小值为2.
以CQ为直径作⊙O,当⊙O与AB边相切动点P时,CQ最短,
∴OP⊥AB,
∵∠ACB=90°,∠A=30°,
∴∠POA=60°,
∵OP=OQ,
∴△POQ为等边三角形,
∴∠POQ=60°,
∴∠APQ=30°,
∴设PQ=OQ=AP=OC=r,3r=AC=cos30°AB=![]() =3,
=3,
∴CQ=2,
∴CQ的最小值为2.
故答案为2.

练习册系列答案
相关题目