题目内容
【题目】在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.
(1)点P和Q互为正交点,P的坐标为(﹣2,3),
①如果Q的坐标为(6,m),那么m的值为多少;
②如果Q的坐标为(x,y),求y与x之间的关系式;
(2)点M和N互为正交点,直接写出∠MON的度数;
(3)点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.
【答案】(1)①m=4,②y=![]() x;(2)∠MON=90°;(3)符合条件的OE的范围为:2
x;(2)∠MON=90°;(3)符合条件的OE的范围为:2![]() ﹣2≤OE≤2+2
﹣2≤OE≤2+2![]() .
.
【解析】
(1)①②根据互为正交点的定义,列出方程即可解决问题;
(2)设M(m,n),N(p,q),推出直线OM的解析式为y=![]() x,直线ON的解析式为y=
x,直线ON的解析式为y=![]() x,由点M和N互为正交点,可得mp+nq=0,推出kOMkON=
x,由点M和N互为正交点,可得mp+nq=0,推出kOMkON=![]() =﹣1即可解决问题;
=﹣1即可解决问题;
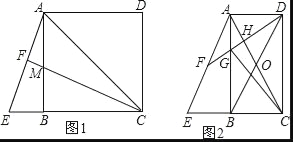
(3)如图1中,连接EF交CD于H,作FQ⊥CD于Q.寻找特殊位置,求出OE的最大值以及最小值即可.
(1)①由题意:﹣2×6+3m=0,
解得m=4,
故答案为4.
②由题意:﹣2x+3y=0,
∴y=![]() x.
x.
(2)设M(m,n),N(p,q),
∴直线OM的解析式为y=![]() x,直线ON的解析式为y=
x,直线ON的解析式为y=![]() x,
x,
∵点M和N互为正交点,
∴mp+nq=0,
∴kOMkON=![]() =﹣1,
=﹣1,
∴OM⊥ON.
∴∠MON=90°.
(3)如图1中,连接EF交CD于H,作FQ⊥CD于Q.
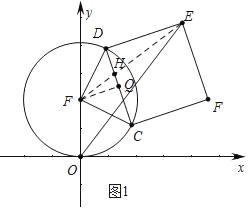
由题意DF=CF=2,CD=DE=2![]() ,DQ=QC=FQ=
,DQ=QC=FQ=![]() ,
,
∵FQ∥DE,
∴QH:DH=FQ:DE=FH:EH=1:2,
∴HQ=![]() ,FH=
,FH=![]() ,
,
∴EH=2FH=![]() ,
,
∴EF=FH+EH=2![]() ,
,
在△OFE中,EF﹣OF≤OE≤EF+OF,
∴当点E在y轴的正半轴上时,O、F、E共线,此时OE的值最大,最大值为2+2![]() .
.
∵原点O在正方形CDEF的外部,
∴当点E在y轴负半轴上时,OE的值最小,最小值为2![]() ﹣2.
﹣2.
∴符合条件的OE的范围为:2![]() ﹣2≤OE≤2+2
﹣2≤OE≤2+2![]() .
.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.