题目内容
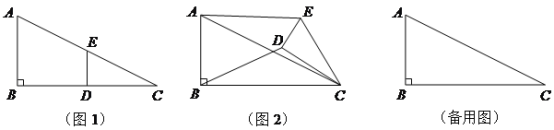
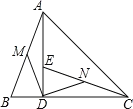
【题目】如图,在![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,求
的中点,求![]() 的度数.
的度数.

【答案】90°
【解析】
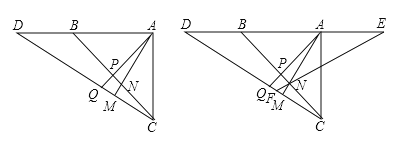
由垂直的定义得到∠ADB=∠ADC=90°,根据SAS可得△ABD≌△CDE;根据全等三角形的性质得到∠BAD=∠DCE,根据直角三角形的性质得到AM=CN,由△ADM≌△CDN,可得∠ADM=∠CDN,再根据∠CDN+∠ADN=90°,可得∠ADM+∠ADN=90°,即可得出∠MDN=90°.
∵AD⊥BC,∴∠ADB=∠ADC=90°.在△ABD与△CDE中,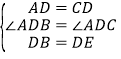 ,∴△ABD≌△CDE(SAS),∴∠BAD=∠DCE,AB=CE.
,∴△ABD≌△CDE(SAS),∴∠BAD=∠DCE,AB=CE.
∵M、N分别是AB、CE的中点,∴AM![]() AB,CN
AB,CN![]() CE,∴AM=CN.在△ADM和△CDN中,
CE,∴AM=CN.在△ADM和△CDN中,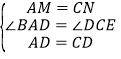 ,∴△ADM≌△CDN(SAS),∴∠ADM=∠CDN.
,∴△ADM≌△CDN(SAS),∴∠ADM=∠CDN.
∵∠CDN+∠ADN=90°,∴∠ADM+∠ADN=90°,∴∠MDN=90°.

练习册系列答案
相关题目