题目内容
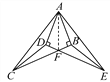
【题目】如图,∠ABC=∠ADE=90°,AD=AB,AC=AE,BC与DE相交于点F,连接CD、EB.
(1)图中共有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
【答案】(1)有三对全等三角形,具体见解析;(2)证明见解析.
【解析】试题分析:(1)根据全等三角形的判定,结合图形得出即可;
(2)连接AF,根据HL证Rt△ABC≌Rt△ADE推出BC=DE,根据HL推出△ADF≌△ABF,推出DF=BF,利用线段的差即可得.
试题解析:(1) 图中有3对全等三角形有Rt△ABC≌Rt△ADE,△ACD≌△AEB,△CDF≌△EBF;
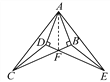
(2)连接AF,
∵∠ABC=∠ADE=90°,AB=AD,AC=AE,
∴Rt△ABC≌Rt△ADE(HL),
∴BC=DE,
在Rt△ABF和Rt△ADF中,AB=AD,AF=AF,
∴Rt△ABF≌Rt△ADF(HL),
∴BF=DF,
∴BC-BF=DE-DF,
即CF=EF.

练习册系列答案
相关题目




