题目内容
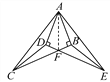
【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
【答案】(1)150°;(2)30°+![]() α.
α.
【解析】分析:(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;
(2)如图2,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E的数量关系;
(3)根据四边形内角和为360°,再根据(2)的结论,以及角平分线的定义即可求解.
详解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-90°-120°=150°;

(2)如图2,过O点作OF∥CD,
∵CD∥OE,
∴OF∥OE,
∴∠AOF=180°-∠OCD,∠BOF=∠EO′O=180°-∠BO′E,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E=360°-(∠OCD+∠BO′E)=120°,
∴∠OCD+∠BO′E=240°;
(3)∵CP是∠OCD的平分线,
∴∠OCP=![]() ∠OCD,
∠OCD,
∴∠CPO′=360°-90°-120°-∠OCP
=150°-![]() ∠OCD
∠OCD
=150°-![]() (240°-∠BO′E)
(240°-∠BO′E)
=30°+![]() α.
α.

练习册系列答案
相关题目