题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ![]() ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( )
A.4π
B.2π
C.π
D.![]()
【答案】D
【解析】解:连接OD.
∵CD⊥AB,
∴CE=DE= ![]() CD=
CD= ![]() (垂径定理),
(垂径定理),
故S△OCE=S△ODE ,
即可得阴影部分的面积等于扇形OBD的面积,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD= ![]() =
= ![]() ,即阴影部分的面积为
,即阴影部分的面积为 ![]() .
.
故选:D.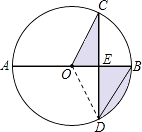
【考点精析】根据题目的已知条件,利用垂径定理和圆周角定理的相关知识可以得到问题的答案,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目