题目内容
【题目】如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE= . 
【答案】![]() ﹣1
﹣1
【解析】解:过E作EF⊥DC于F, ∵四边形ABCD是正方形,
∴AC⊥BD,
∵CE平分∠ACD交BD于点E,
∴EO=EF,
在Rt△COE和Rt△CFE中![]() ,
,
∴Rt△COE≌Rt△CFE(HL),
∴CO=FC,
∵正方形ABCD的边长为1,
∴AC= ![]() ,
,
∴CO= ![]() AC=
AC= ![]() ,
,
∴CF=CO= ![]() ,
,
∴EF=DF=DC﹣CF=1﹣ ![]() ,
,
∴DE= ![]() =
= ![]() ﹣1,
﹣1,
另法:因为四边形ABCD是正方形,
∴∠ACB=45°=∠DBC=∠DAC,
∵CE平分∠ACD交BD于点E,
∴∠ACE=∠DCE=22.5°,
∴∠BCE=45°+22.5°=67.5°,
∵∠CBE=45°,
∴∠BEC=67.5°,
∴BE=BC,
∵正方形ABCD的边长为1,
∴BC=1,
∴BE=1,
∵正方形ABCD的边长为1,
∴AC= ![]() ,
,
∴DE= ![]() ﹣1,
﹣1,
故答案为: ![]() ﹣1.
﹣1.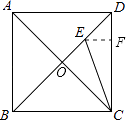
过E作EF⊥DC于F,根据正方形的性质和角平分线的性质以及勾股定理即可求出DE的长.

练习册系列答案
相关题目