��Ŀ����
����Ŀ����ͼ��ʾ���߶�AB=6cm��C���P�������1cm/s���ٶ���AB�����˶���D���B������2cm/s���ٶ���AB�����˶���C���߶�AP�ϣ�D���߶�BP�ϣ� 
��1����C��D�˶�������ʱ�̶���PD=2AC�����P��AB�ϵ�λ�ã�
��2���ڣ�1���������£�Q��ֱ��AB��һ�㣬��AQ��BQ=PQ����PQ��ֵ��
��3���ڣ�1���������£���C��D�˶���һ��ʱ���ǡ��AB=2CD����ʱ��Cֹͣ�˶�����������߶�PB���˶���M��N�ֱ���CD��PD���е㣬���MN��ֵ��
���𰸡�
��1���⣺����C��D���˶��ٶ�֪��BD=2PC��
��PD=2AC��
��BD+PD=2��PC+AC������PB=2AP��
���P���߶�AB�ϵ� ![]() ��
��
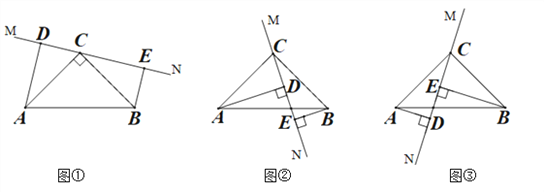
��2���⣺��ͼ1��
��AQ��BQ=PQ��
��AQ=PQ+BQ��
�֡�AQ=AP+PQ��
��AP=BQ��
��PQ= ![]() AB=2cm��
AB=2cm��
����Q'��AB���ӳ�����ʱ��
AQ�䩁AP=PQ�䣬
����AQ�䩁BQ��=PQ=AB=6cm��
����������PQ=2cm��6cm
![]()
��3���⣺MN��ֵ���䣮
���ɣ���ͼ2����C��ֹͣ�˶�ʱ����CD= ![]() AB=3cm��
AB=3cm��
��AC+BD= ![]() AB=3cm��
AB=3cm��
��AP��PC+BD= ![]() AB=3cm��
AB=3cm��
��AP= ![]() AB=2cm��PC=5cm��BD=10cm��
AB=2cm��PC=5cm��BD=10cm��
��M��CD�е㣬N��PD�е㣬
��MN=MD��ND= ![]() CD��
CD�� ![]() PD=
PD= ![]() CP=
CP= ![]() cm��
cm��
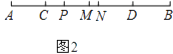
����������1������C��D���˶��ٶ�֪BD=2PC��������֪����PD=2AC���PB=2AP�����Ե�P���߶�AB�ϵ� ![]() ������2�������軭��ͼʾ������AQ��BQ=PQ���AQ=PQ+BQ��Ȼ�����AP=BQ���Ӷ����PQ��AB�Ĺ�ϵ����3����C��ֹͣ�˶�ʱ����CD=
������2�������軭��ͼʾ������AQ��BQ=PQ���AQ=PQ+BQ��Ȼ�����AP=BQ���Ӷ����PQ��AB�Ĺ�ϵ����3����C��ֹͣ�˶�ʱ����CD= ![]() AB����AC+BD=
AB����AC+BD= ![]() AB������AP��PC+BD=
AB������AP��PC+BD= ![]() AB������AP=
AB������AP= ![]() AB��PC=5cm��BD=10cm���ٸ���M��CD�е㣬N��PD�е�ɵó�MN�ij��������ɵó����ۣ�
AB��PC=5cm��BD=10cm���ٸ���M��CD�е㣬N��PD�е�ɵó�MN�ij��������ɵó����ۣ�
�����㾫����������Ҫ�����������ľ�������֪ʶ�㣬��Ҫ����ͬ����������룬���С����Ϊ֮������Ⱦ������㣬���������ˣ�ƽ�����������㣬���ݱ������ֵ�����ӿ�ƽ�������빫ʽҪ�μDz�����ȷ�����⣮

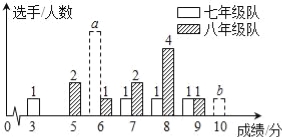
����Ŀ��2015��10��29�գ�����ʮ�˽�����ȫ��ʤ����Ļ��ij��ѧ�ߡ����꼶��ѡ��10��ѡ�ֲμ�������ʮ�˽�����ȫ��֪ʶ�������Ʒֲ���10���ƣ�ѡ�ֵ÷־�Ϊ�������ɼ��ﵽ6�ֻ�6������Ϊ�ϸﵽ9�ֻ�10��Ϊ���㣮��ξ������ߡ����꼶��֧������ѡ�ֳɼ��ֲ�������ͳ��ͼ�ͳɼ�ͳ�Ʒ��������£��������꼶�����ӵ�6�֡�10�ֵ�ѡ�������ֱ�Ϊa��b��
�ӱ� | ƽ���� | ��λ�� | ���� | �ϸ��� | ������ |
���꼶 | 6.7 | m | 3.41 | 90% | n |
���꼶 | 7.1 | 7.5 | 1.69 | 80% | 10% |
��1��������ͼ���е����ݣ���a��b��ֵ��
��2��ֱ��д�����е�m= ��n= ��
��3������˵���꼶�ĺϸ��ʡ������ʾ����ڰ��꼶���������꼶�ӳɼ��Ȱ��꼶�Ӻã���Ҳ����˵���꼶�ӳɼ������꼶�Ӻã������������֧�ְ��꼶�ӳɼ��õ����ɣ�