��Ŀ����
����Ŀ������ABC�У���ACB=90��AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E.
(1)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ����֤��DE=AD+BE��
(2)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ�����ʣ�DE��AD��BE�������ĵ�����ϵ����д�����������ϵ��������֤��.
(3)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ��DE��AD��BE֮��ĵ�����ϵ�� (ֱ��д���𰸣�����֤��.)
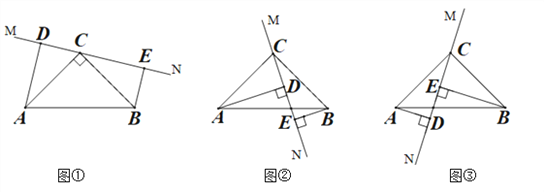
���𰸡���1��֤������������2��AD-BE=DE��֤������������3��BE-AD=DE.
�����������������
��1������֪������֤��DAC�͡�DCA���࣬��ECB�͡�DCA���࣬�ɴ˿ɵá�DAC=��ECB�����������������֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ϳ�֤�ã�DE=DC+CE=AD+BE��
��2���ɣ�1����˼·֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ӷ��ɵã�DE=CE-CD=AD-BE��
��3��ͬ��2����˼·֤��ADC�͡�CEBȫ�ȿɵ�AD=CE��CD=BE���Ӷ��ɵã�DE=CD-CE=BE-AD.
���������
��1����AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У� 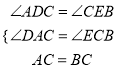 ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=DC+CE��
��DE=AD+BE.
��2����ͼ�ڣ�DE��AD��BE�Ĺ�ϵΪ��DE=AD-BE.�������£�
��AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У�  ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=CE-CD��
��DE=AD-BE.
��3����ͼ����DE��AD��BE֮��ĵ�����ϵ����DE=BE-AD���������£�
��AD��MN��D��BE��MN��E��
���ADC=��CEB=90����
�֡ߡ�ACB=90�㣬
���DAC+��ACD=90������ECB+��ACD=90����
���DAC=��ECB��
����ADC�͡�CEB�У�  ��
��
���ADC�ա�CEB��
��AD=CE��DC=BE��
����DE=CD-CE��
��DE=BE-AD.

 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�