题目内容
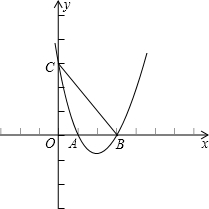
如图,已知抛物线经过点B(-2,3),原点O和x轴上另一点A,它的对称轴与x轴交于点C (2,0).
(2,0).
(1)求此抛物线的函数关系式;
(2)连接CB,在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标;
(3)在(2)的条件下,连接BE,设BE的中点为G,在抛物线的对称轴上是否存在点P,使得△PBG的周长最小?若存在,求出P点坐标;若不存在,请说明理由.
 (2,0).
(2,0).(1)求此抛物线的函数关系式;
(2)连接CB,在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标;
(3)在(2)的条件下,连接BE,设BE的中点为G,在抛物线的对称轴上是否存在点P,使得△PBG的周长最小?若存在,求出P点坐标;若不存在,请说明理由.
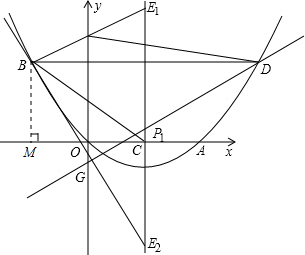
(1)由题意知:A(4,0);
设抛物线的解析式为y=ax(x-4),已知抛物线过B(-2,3);则有:
3=ax(-2)×(-2-4),
a=
∴抛物线的解析式为:y=
x2-x;
(2)过点B作BM⊥MC,
∵B点坐标为:(-2,3),C点坐标为:(2,0),
∴MC=4,BM=3,
BC=
=5,
∴|CE|=5,
∴E1(2,5),E2(2,-5);
(3)存在.
①当E1(2,5)时,G1(0,4),设点B关于直线x=2的对称点为D,
其坐标为(6,3)
直线DG1的解析式为:y=-
x+4,
∴P1(2,
)
②当E2(2,-5)时,G2(0,-1),直线DG2的解析式为:y=
x-1
∴P2(2,
)
综合①、②存在这样的点P,使得△PBG的周长最小,且点P的坐标为(2,
)
或(2,
).
设抛物线的解析式为y=ax(x-4),已知抛物线过B(-2,3);则有:
3=ax(-2)×(-2-4),
a=
| 1 |
| 4 |
∴抛物线的解析式为:y=
| 1 |
| 4 |
(2)过点B作BM⊥MC,
∵B点坐标为:(-2,3),C点坐标为:(2,0),
∴MC=4,BM=3,
BC=
| BM2+MC2 |
∴|CE|=5,
∴E1(2,5),E2(2,-5);
(3)存在.
①当E1(2,5)时,G1(0,4),设点B关于直线x=2的对称点为D,
其坐标为(6,3)
直线DG1的解析式为:y=-
| 1 |
| 6 |
∴P1(2,
| 11 |
| 3 |
②当E2(2,-5)时,G2(0,-1),直线DG2的解析式为:y=
| 2 |
| 3 |
∴P2(2,
| 1 |
| 3 |
综合①、②存在这样的点P,使得△PBG的周长最小,且点P的坐标为(2,
| 11 |
| 3 |
或(2,
| 1 |
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


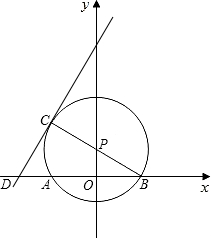 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为