题目内容
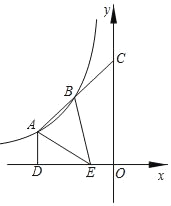
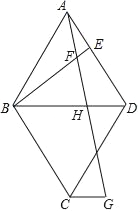
【题目】如图,菱形ABCD中,∠BAD=60°,点E在边AD上,连接BE,在BE上取点F,连接AF并延长交BD于H,且∠AFE=60°,过C作CG∥BD,直线CG、AF交于G.
(1)求证:∠FAE=∠EBA;
(2)求证:AH=BE;
(3)若AE=3,BH=5,求线段FG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)FG=![]() .
.
【解析】
(1)先证明两三角形相似,再根据性质得到结果(2)先证明两三角形相似,再根据性质得到边的关系(3)先作辅助线,再证明两三角形相似,再根据相似三角形性质得到结果.
解:(1)∵∠AFE=∠BAE=60°、∠AEF=∠BEA,
∴△AEF∽△BEA,
∴∠FAE=∠ABE;
(2)∵四边形ABCD是菱形,且∠BAD=60°,
∴AB=AD、∠BAE=∠ADB=60°,
在△ABE和△DAH中,
∵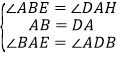
∴△ABE≌△DAH(ASA),
∴AH=BE;
(3)如图,连接AC交BD于点P,则AC⊥BD,且AC平分BD,
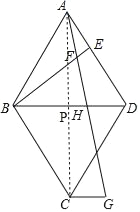
∵△ABE≌△DAH,
∴AE=DH=3,
则BD=BH+DH=8,
∴BP=PD=4,PH=BH﹣BP=1,
∵AB=BD=8,
∴AP=![]() =4
=4![]() ,
,
则AC=2AP=8![]() ,
,
∵CG∥BD,且P为AC中点,
∴∠ACG=90°,CG=2PH=2,
∴AG=![]() =14,BE=AH=
=14,BE=AH=![]() AG=7,
AG=7,
∵△AEF∽△BEA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:AF=![]() ,
,
∴FG=AG﹣AF=14﹣![]() =
=![]() .
.

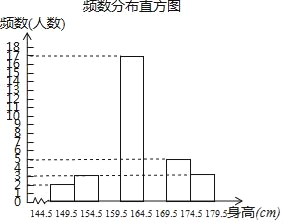
【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?