��Ŀ����
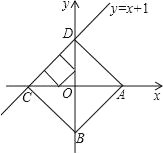
����Ŀ����ͼ��������ABCD��һ�κ���y��x+1ͼ�������һ�����������Σ�
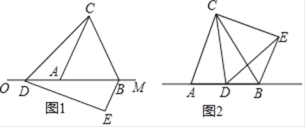
��1����ij������һ�κ���y��x+1��������ͼ������а��������εı߳���
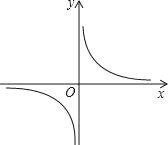
��2����ij�����Ƿ���������![]() ������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
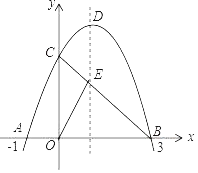
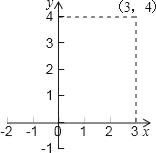
��3����ij�����Ƕ��κ���y��ax2+c��a��0��������ͼ��İ���������ΪABCD��C��D�е�һ��������Ϊ��3��4����д���������������������ϵ���һ���������꣬д���������������һ�������߽���ʽ�����ж���д���������ߵİ��������εĸ�������������ż����������С��ֻ��ֱ��д���𰸣�
���𰸡���1�������α߳�Ϊ![]() ����2��m��1��y��
����2��m��1��y��![]() ����3��D��������1��3����y��
����3��D��������1��3����y��![]() x2+
x2+ ![]() ��������κ������ߵİ��������θ���Ϊż����
��������κ������ߵİ��������θ���Ϊż����
��������
�����Ϊ��ӱ���ر�Ҫע������ͷ������⣬���İ�����֪꣬A��BΪ�����������㣬C��DΪ����ͼ���ϵ����㣺��1������ȷ�ػ���ͼ�Σ������������ε�����ȷ����ص������Ӷ����������εı߳���ע��˼ά�������ԣ�
��2����ΪABCDΪ�����Σ����Կ������ߵõ�����ֱ�������Σ����õ�D��2��m���������ʾ����C������Ӷ���⣮
��3��ע��˼ά�������ԣ������߿��ڼȿ������ϣ�Ҳ�������£��������߿�������ʱ�������ε���һ������Ҳ�����������ϣ������ȿ����ڵ㣨3��4������ߣ�Ҳ�����ڵ㣨3��4�����ұߣ����㣨3��4����x�������ߣ�����ȫ��������ȷ���߶εij�����ȷ������������һ��������ꣻ�������߿�������ʱҲ��һ���ط�Ϊ������������ۣ�
��1����������ABCD��һ�κ���y��x+1ͼ�������һ�����������Σ�
����A��x�������ᡢ��B��y�Ḻ������ʱ��
��AO��1��BO��1��
��������ABCD�ı߳�Ϊ![]()
����A��x�Ḻ���ᡢ��B��y����������ʱ����������ABCD�ı߳�Ϊa����3a��![]()
��a=![]()
![]() ,���������α߳�Ϊ
,���������α߳�Ϊ![]()
![]() ��
��
��2����DE��CF�ֱ�ֱ��x��y�ᣬ
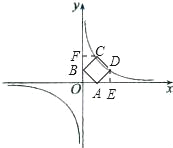
֪��ADE�ա�BAO�ա�CBF����ʱ��m��2��DE��OA��BF��m��OB��CF��AE��2��m
��OF��BF+OB��2
��C��������2��m��2��
��2m��2��2��m��
���m��1��
�෴���������Ľ���ʽΪy��![]() ��
��
��3���������⻭��ͼ�Σ���ͼ��ʾ��
��C��CF��x�ᣬ����ΪF����D��DE��CF������ΪE��
���CED�ա�DGB�ա�AOB�ա�AFC��
��C��3��4������CF��4��OF��3��
��EG��3��DE��4����DG��DE��GE��DE��OF��4��3��1����D����Ϊ����1��3�������D��C�������ߵĽ���ʽΪ��y��ax2+b��
��D��C���������ã�![]() ��
��
���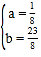 ��
��
����������������ߵĽ���ʽΪy��![]() x2+
x2+![]() ��
��
ͬ���ɵ�D���������Ϊ����7����3��������4��7������4��1������Ӧ�������߷ֱ�Ϊy=![]() x2+
x2+![]() ��y=
��y=![]() x2+
x2+![]() ��y=
��y=![]() x2+
x2+![]() ��������κ������ߵİ��������θ���Ϊż����
��������κ������ߵİ��������θ���Ϊż����

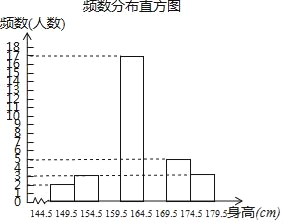
����Ŀ��Ϊ�˽�ͬѧ�ǵ����巢�������ѧУ�����칫�Ҷ����꼶ȫ��ѧ�����������߲�������ȷ��1cm���������г�ȡ�˲������ݽ���ͳ�ƣ��������δ��ɵ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������⣺
Ƶ�ʷֲ���
���� | Ƶ�� | �ٷֱ� |
144.5��149.5 | 2 | 4% |
149.5��154.5 | 3 | 6% |
154.5��159.5 | a | 16% |
159.5��164.5 | 17 | 34% |
164.5��169.5 | b | n% |
169.5��174.5 | 5 | 10% |
174.5��179.5 | 3 | 6% |
��1����a��b��n��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��ѧУ�������꼶ѧ����ѡ�λ����֣�Ҫ�����߲�����170cm��������꼶��ѧ��350�ˣ������ֵĺ�ѡ�˴���ж��٣�