题目内容
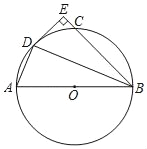
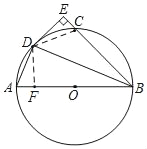
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,BC=4,求CE的长.
【答案】(1)DE与⊙O相切,证明详见解析;(2)EC=1.
【解析】
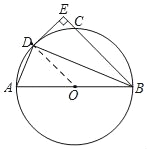
(1)连接OD,由题意可得∠CBD=∠ODB=∠DBO,可得OD∥BE,可证DE⊥OD,即可证DE与⊙O相切;
(2)过点D作DF⊥AB于点F,连接DC,由题意可证Rt△DFA≌Rt△DEC,Rt△DBF≌Rt△DBE,可得AF=EC,BF=BE,即可求EC的长.
解:(1)DE与⊙O相切
理由如下:连接OD
∵OB=OD
∴∠OBD=∠ODB
∵∠ABC的平分线交⊙O于点D,
∴∠ABD=∠CBD
∴∠CBD=∠ODB
∴OD∥BE
∵DE⊥BC于点E.
∴DE⊥OD
∴DE与⊙O相切
(2)过点D作DF⊥AB于点F,连接DC,
∵∠ABD=∠CBD,DE⊥BE,DF⊥AB
∴DF=DE,![]()
∴AD=CD
∵AD=CD,DF=DE
∴Rt△DFA≌Rt△DEC(HL)
∴AF=EC
∵DF=DE,DB=DB
∴Rt△DBF≌Rt△DBE(HL)
∴BF=BE
∵BA=BF+AF=BE+AF=BC+EC+CE=6
∴4+2CE=6
∴EC=1

练习册系列答案
相关题目