题目内容
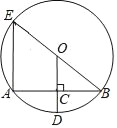
【题目】如图所示,△ABC是边长为2的等边三角形,D是AB边的中点,F是BC边上的动点,E是AC边上的动点,当E、F的位置在何处时,才能使![]() 的周长最小?简要说明作法.
的周长最小?简要说明作法.

【答案】点E、F分别为AC、BC中点时,△DEF的周长最小.
【解析】
分别作点D关于BC、AC的对称点D1、D2,交AC、BC于M、N,连接![]() ,分别交AC、BC于点E、F,根据轴对称的性质可得DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,D1D2是△DEF的最小值,由等边三角形的性质可得∠B=∠A=60°,可得∠ADM=∠BDN=30°,即可得∠D1DD2=120°,利用ASA可证明△ADM≌△BDN,可得DD2=DD1,根据等腰三角形的性质可得∠D1=∠D2=30°,即可证明∠D1=∠ADM,利用ASA可证明△ADM≌△ED1M,可得AM=EM,可证明AD=AE,即可证明点E为AC的中点,同理可得点F为BC的中点,可得答案.
,分别交AC、BC于点E、F,根据轴对称的性质可得DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,D1D2是△DEF的最小值,由等边三角形的性质可得∠B=∠A=60°,可得∠ADM=∠BDN=30°,即可得∠D1DD2=120°,利用ASA可证明△ADM≌△BDN,可得DD2=DD1,根据等腰三角形的性质可得∠D1=∠D2=30°,即可证明∠D1=∠ADM,利用ASA可证明△ADM≌△ED1M,可得AM=EM,可证明AD=AE,即可证明点E为AC的中点,同理可得点F为BC的中点,可得答案.
如图所示,作点D关于AC的对称点D1,作点D关于BC的对称点![]() ,交AC、BC于M、N,连接
,交AC、BC于M、N,连接![]() ,分别交AC、BC于点E、F,
,分别交AC、BC于点E、F,
∴DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,
∴DE+DF+EF=D1E+EF+D2F=D1D2,
∴D1D2即是△DEF的最小值,则点E、F即为所求,
∵△ABC是等边三角形,
∴∠A=∠B=60°,
∴∠ADM=∠BDN=90°-60°=30°,
∴∠D1DD2=180°-30°-30°=120°,
∵点D为AB中点,
∴AD=BD,
在△BDN和△ADM中,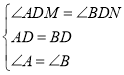 ,
,
∴△ADM≌△BDN,
∴DN=DM,
∴DD2=DD1,
∴∠D1=∠D2=30°,
∴∠D1=∠ADM,
在△ADM和△ED1M中,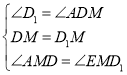 ,
,
∴△ADM≌△ED1M,
∴AM=EM,
∵∠ADM=30°,DM⊥AC,
∴AM=![]() AD,
AD,
∴AE=AD,
∴点E为AC中点,
同理可得:点F为BC中点,
∴点E、F分别为AC、BC中点时,△DEF的周长最小.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
出厂价 | 成本价 | 排污处理费 | |
甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 另每月还需支付设备管理、维护费20000元 |
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?