题目内容
【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．
【答案】36°或37°．
【解析】分析：先过E作EG∥AB，根据平行线的性质可得∠AEF=∠BAE+∠DFE，再设∠CEF=x，则∠AEC=2x，根据6°＜∠BAE＜15°，即可得到6°＜3x-60°＜15°，解得22°＜x＜25°，进而得到∠C的度数．
详解：如图，过E作EG∥AB，
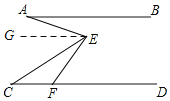
∵AB∥CD，
∴GE∥CD，
∴∠BAE=∠AEG，∠DFE=∠GEF，
∴∠AEF=∠BAE+∠DFE，
设∠CEF=x，则∠AEC=2x，
∴x+2x=∠BAE+60°，
∴∠BAE=3x-60°，
又∵6°＜∠BAE＜15°，
∴6°＜3x-60°＜15°，
解得22°＜x＜25°，
又∵∠DFE是△CEF的外角，∠C的度数为整数，
∴∠C=60°-23°=37°或∠C=60°-24°=36°，
故答案为：36°或37°．
名校课堂系列答案
【题目】画出函数
的图象.
（1）函数
的自变量x的取值范围是________；
（2）列表（把表格补充完整）
x | …… | -2 | -1 | 0 | 1 | 2 | 3 | 4 | …… |
y |
（3）描点、连线
（4）结合图象，写出函数的一条性质________________________________________.
【题目】为了推进我市校园体育运动的发展，2017年义乌市中小学运动会在雪峰中学成功举办．在此期间，某体育文化用品商店计划一次性购进篮球和排球共60个，其进价与售价间的关系如下表：
篮球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 105 | 70 |
（1）商店用4200元购进这批篮球和排球，求购进篮球和排球各多少个？
（2）设商店所获利润为y（单位：元），购进篮球的个数为x（单位：个），请写出y与x之间的函数关系式（不要求写出x的取值范围）；
（3）若要使商店的进货成本在4300元的限额内，且全部销售完后所获利润不低于1400元，请你列举出商店所有进货方案，并求出最大利润是多少？
