题目内容
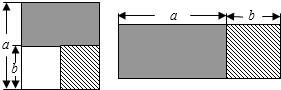
如图，边长为a的正方形中有一个边长为b的小正方形，若将图1的阴影部分拼成一个长方形，如图2，比较图1和图2的阴影部分的面积，你能得到的公式是______．
根据题意得：
图1中阴影部分的面积为：a2-b2；
图2中阴影部分的面积为：（a+b）（a-b）．
∵两图形阴影面积相等，
∴可以得到的结论是：a2-b2=（a+b）（a-b）．
故答案为：a2-b2=（a+b）（a-b）．
图1中阴影部分的面积为：a2-b2；
图2中阴影部分的面积为：（a+b）（a-b）．
∵两图形阴影面积相等，
∴可以得到的结论是：a2-b2=（a+b）（a-b）．
故答案为：a2-b2=（a+b）（a-b）．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
