题目内容
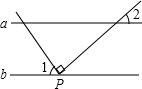
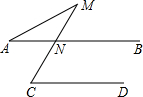
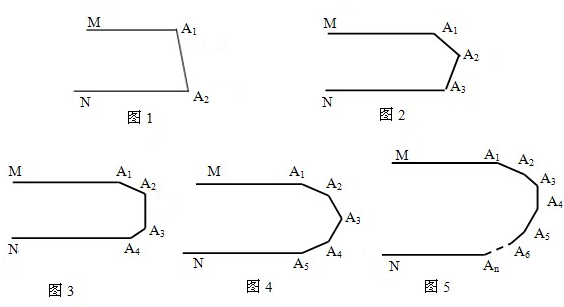
如图1,MA1∥NA2,则∠A1+∠A2=______度.
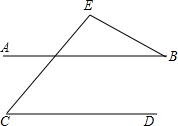
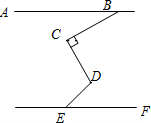
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=______度.
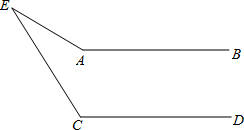
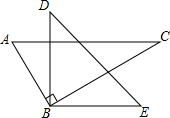
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=______度.
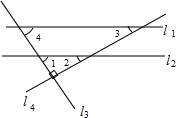
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=______度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=______度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=______度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=______度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=______度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=______度.

如图1,
∵MA1∥NA2,
∴∠A1+∠A2=180°.
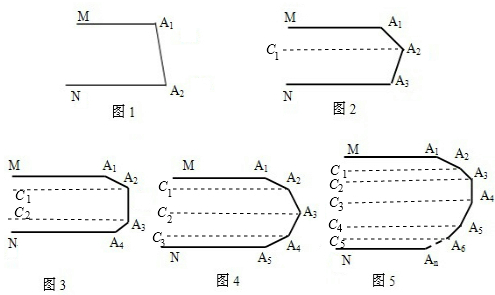
如图2,过点A2作A2C1∥A1M,
∵MA1∥NA3,
∴A2C1∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A3=180°,
∴∠A1+∠A2+∠A3=360°.
如图3,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,
∵MA1∥NA3,
∴A2C1∥A3C2∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A4=180°,
∴∠A1+∠A2+∠A3+∠A4=540°.
如图4,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,
∵MA1∥NA3,
∴A2C1∥A3C2∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A3A4C3=180°∠C3A4A5+∠A5=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=720°.
从上述结论中你发现了规律:如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=180(n-1)度.
故答案为:180,360,540,720,180(n-1).

练习册系列答案
相关题目