题目内容
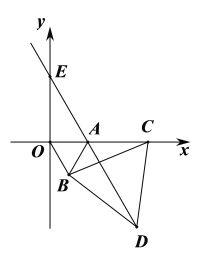
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,点
,点![]() 为
为![]() 正半轴上一动点
正半轴上一动点![]() , 连接
, 连接![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的度数是否会变化?如果不变,请求出
的度数是否会变化?如果不变,请求出![]() 的度数;如果变化,请说明理由.
的度数;如果变化,请说明理由.
(3)当点![]() 运动到什么位置时,以
运动到什么位置时,以![]() 为顶点的三角形是等腰三角形?
为顶点的三角形是等腰三角形?
【答案】![]() 详见解析;
详见解析;![]() 的度数不会变化,
的度数不会变化,![]() ;
;![]() 当点
当点![]() 运动到
运动到![]() 时.
时.
【解析】
(1)根据等边三角形的性质可得BO=BA,BC=BD,∠OBA=∠CBD=60°,进而可利用SAS证明![]() ≌
≌![]() ;
;
(2)设BC、DE交于点F,如图1,根据全等三角形的性质可得∠1=∠2,根据三角形的内角和定理可得∠CAD=∠CBD,进而可得结论;
(3)易求得∠EAC=120°,∠OEA=30°,即得以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰,然后根据30°角的直角三角形的性质可得AE的长,进而可得AC、OC的长,即可得出点C的位置.
解:(1)证明:∵△AOB、△BCD是等边三角形,
∴BO=BA,BC=BD,∠OBA=∠CBD=60°,
∴∠OBC=∠ABD,
∴![]() ≌
≌![]() (SAS);
(SAS);
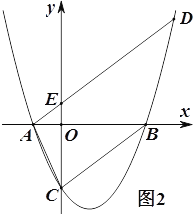
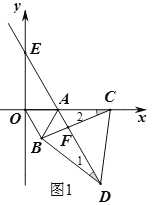
(2)设BC、DE交于点F,如图1,
∵![]() ≌
≌![]() ,∴∠1=∠2,
,∴∠1=∠2,
∵∠AFC=∠BFD,∴∠CAD=∠CBD=60°,
∴![]() 的度数不会变化,且
的度数不会变化,且![]() ;
;
(3)∵![]() ,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
∴以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰,
∵在Rt△AOE中,OA=1,∠OEA=30°,∴AE=2,
∴AC=AE=2,∴OC=1+2=3,
∴当点C的坐标为(3,0)时,以A,E,C为顶点的三角形是等腰三角形.

练习册系列答案
相关题目