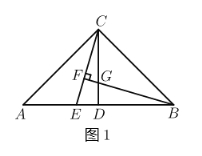
题目内容
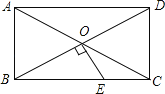
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,折痕
处,称为第1次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,折痕
处,称为第2次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,按上述方法不断操作下去…经过第2020次操作后得到的折痕
,按上述方法不断操作下去…经过第2020次操作后得到的折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为______.
的值为______.
【答案】![]()
【解析】
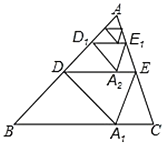
根据中点的性质及折叠的性质可得DA=DA=DB,从而可得∠ADA=2∠B,结合折叠的性质可得.,∠ADA=2∠ADE,可得∠ADE=∠B,继而判断DE//BC,得出DE是△ABC的中位线,证得AA⊥BC,AA=2,由此发现规律:![]() 同理
同理![]()
![]() …于是经过第n次操作后得到的折痕Dn-1En-1到BC的距离
…于是经过第n次操作后得到的折痕Dn-1En-1到BC的距离![]() ,据此求得
,据此求得![]() 的值.
的值.
解:如图连接AA ,由折叠的性质可得:AA ⊥DE, DA=DA,A、A…均在AA 上
又∵D是AB中点,∴DA=DB, 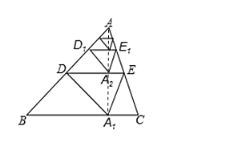
∵DB=DA ,
∴∠BA D=∠B,
∴∠ADA =∠B +∠BA D=2∠B,
又∵∠ADA =2∠ADE,
∴∠ADE=∠B
∵DE//BC,
∴AA⊥BC,
∵h=1
∴AA=2,
∴![]()
同理:![]() ;
;![]() ;
;
…
∴经过n次操作后得到的折痕Dn-1En-1到BC的距离![]()
∴![]()

 阅读快车系列答案
阅读快车系列答案【题目】近期江苏省各地均发布“雾霾”黄色预警,我市某口罩厂商生产一种新型口罩产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系满足下表.
销售单价x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 20 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示y与x的变化规律,并直接写出y与x之间的函数关系式为__________;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?