题目内容
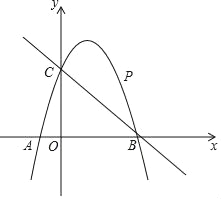
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
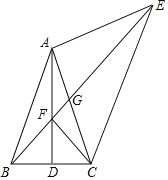
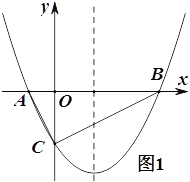
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
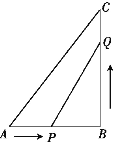
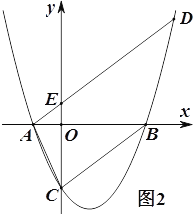
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
【答案】(1)![]() ;(2)点P的坐标为
;(2)点P的坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用三角形相似可求AOOB,再由一元二次方程根与系数关系求AOOB构造方程求n;
(2)求出B、C坐标,设出点Q坐标,利用平行四边形对角线互相平分性质,分类讨论点P坐标,分别代入抛物线解析式,求出Q点坐标;
(3)设出点D坐标(a,b),利用相似表示OA,再由一元二次方程根与系数关系表示OB,得到点B坐标,进而找到b与a关系,代入抛物线求a、n即可.
(1)若△ABC为直角三角形
∴△AOC∽△COB
∴OC2=AOOB
当y=0时,0=![]() x2-
x2-![]() x-n
x-n
由一元二次方程根与系数关系
-OAOB=OC2
n2=![]() =2n
=2n
解得n=0(舍去)或n=2
∴抛物线解析式为y=![]() ;
;
(2)由(1)当![]() =0时
=0时
解得x1=-1,x2=4
∴OA=1,OB=4
∴B(4,0),C(0,-2)
∵抛物线对称轴为直线x=-![]() =
=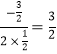
∴设点Q坐标为(![]() ,b)
,b)
由平行四边形性质可知
当BQ、CP为平行四边形对角线时,点P坐标为(![]() ,b+2)
,b+2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,则P点坐标为(
,则P点坐标为(![]() ,
,![]() )
)
当CQ、PB为为平行四边形对角线时,点P坐标为(-![]() ,b-2)
,b-2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,则P坐标为(-
,则P坐标为(-![]() ,
,![]() )
)
综上点P坐标为(![]() ,
,![]() ),(-
),(-![]() ,
,![]() );
);
(3)设点D坐标为(a,b)
∵AE:ED=1:4
则OE=![]() b,OA=
b,OA=![]() a
a
∵AD∥AB
∴△AEO∽△BCO
∵OC=n
∴![]()
∴OB=![]()
由一元二次方程根与系数关系得,![]()
∴b=![]() a2
a2
将点A(-![]() a,0),D(a,
a,0),D(a,![]() a2)代入y=
a2)代入y=![]() x2-
x2-![]() x-n
x-n
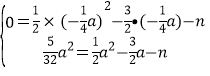
解得a=6或a=0(舍去)
则n=![]() .
.

 智能训练练测考系列答案
智能训练练测考系列答案