题目内容
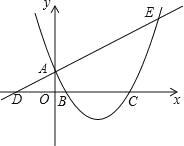
【题目】如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B1,顶点为D1,若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.

【答案】(1)、y=x2﹣3x+2;(2)、y=x2﹣3x+1;(3)、(1,﹣1)或(3,1)
【解析】
试题分析:(1)、利用待定系数法,将点A,B的坐标代入解析式即可求得;(2)、根据旋转的知识可得:A(1,0),B(0,2),∴OA=1,OB=2,可得旋转后C点的坐标为(3,1),当x=3时,由y=x2﹣3x+2得y=2,可知抛物线y=x2﹣3x+2过点(3,2)∴将原抛物线沿y轴向下平移1个单位后过点C.∴平移后的抛物线解析式为:y=x2﹣3x+1;(3)、首先求得B1,D1的坐标,根据图形分别求得即可,要注意利用方程思想.
试题解析:(1)、已知抛物线y=x2+bx+c经过A(1,0),B(0,2),
∴![]() , 解得
, 解得![]() , ∴所求抛物线的解析式为y=x2﹣3x+2;
, ∴所求抛物线的解析式为y=x2﹣3x+2;
(2)、∵A(1,0),B(0,2), ∴OA=1,OB=2, 可得旋转后C点的坐标为(3,1),
当x=3时,由y=x2﹣3x+2得y=2, 可知抛物线y=x2﹣3x+2过点(3,2),
∴将原抛物线沿y轴向下平移1个单位后过点C. ∴平移后的抛物线解析式为:y=x2﹣3x+1;
(3)、∵点N在y=x2﹣3x+1上,可设N点坐标为(x0,x02﹣3x0+1),
将y=x2﹣3x+1配方得y=(x﹣![]() )2﹣
)2﹣![]() ,
,
∴其对称轴为直线x=![]() . ①0≤x0≤
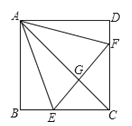
. ①0≤x0≤![]() 时,如图①, ∵
时,如图①, ∵![]() ,
,
∴![]() ∵x0=1, 此时x02﹣3x0+1=﹣1,∴N点的坐标为(1,﹣1).
∵x0=1, 此时x02﹣3x0+1=﹣1,∴N点的坐标为(1,﹣1).
②当![]() 时,如图②, 同理可得
时,如图②, 同理可得![]() , ∴x0=3, 此时x02﹣3x0+1=1,
, ∴x0=3, 此时x02﹣3x0+1=1,
∴点N的坐标为(3,1). ③当x<0时,由图可知,N点不存在, ∴舍去.
综上,点N的坐标为(1,﹣1)或(3,1).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案