题目内容
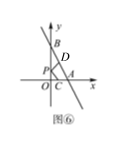
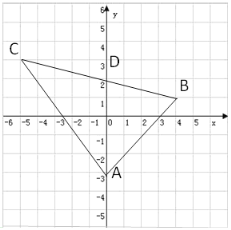
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
【答案】(1)22;(2)M(1,3);(3) ![]() .
.
【解析】
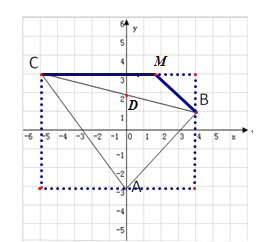
(1)用矩形的面积减去三个直角三角形的面积即可;
(2)根据三角形BCM的面积为6,求出CM的长,进而可求出点M的坐标;
(3)根据三角形ABC的面积=三角形ABD的面积+三角形ACD的面积,求出AD的长,即可求出点D的坐标.
(1)S△ABC =9×6-![]() = 22;
= 22;
(2)∵![]() ,
,
∴CM=6;
∴点M的横坐标=6-5=1,
∴M(1,3);
(3)∵![]() ,
,
∴AD=![]() ,
,
∴OD= ![]() -3=
-3=![]() ,
,
∴![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |