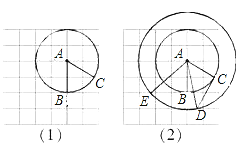��Ŀ����
����Ŀ��С����һ��ֽ�ϻ�һ�����ᣬ���������ϱ��![]() ��
��![]() �����㣬��
�����㣬��![]() ��ʾ������
��ʾ������![]() ����
����![]() ��ʾ������12��
��ʾ������12��
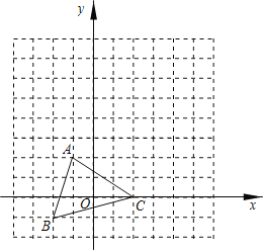
��1���������ϵ�![]() ���
���![]() ���3����λ���ȣ����
���3����λ���ȣ����![]() ����ʾ������
����ʾ������
��2��������ֽ���ۣ�ʹ��![]() ���
���![]() �պ��غϣ��ۺ������ύ�ڵ�
�պ��غϣ��ۺ������ύ�ڵ�![]() �����
�����![]() ��ʾ������
��ʾ������
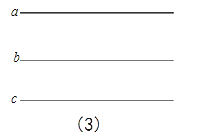
��3����![]() �͵�
�͵�![]() ͬʱ�ӳ�ʼλ�������������˶�����
ͬʱ�ӳ�ʼλ�������������˶�����![]() ���ٶ���ÿ��1����λ���ȣ���
���ٶ���ÿ��1����λ���ȣ���![]() ���ٶ���ÿ��2����λ���ȣ��˶�ʱ����
���ٶ���ÿ��2����λ���ȣ��˶�ʱ����![]() ��.�Ƿ����
��.�Ƿ����![]() ��ֵ��ʹ
��ֵ��ʹ![]() ����
����![]() ��ԭ��ľ�����ڵ�
��ԭ��ľ�����ڵ�![]() ��ԭ��ľ���������������ڣ������
��ԭ��ľ���������������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��-5��-11����2��2����3��![]() ��
��![]()
��������
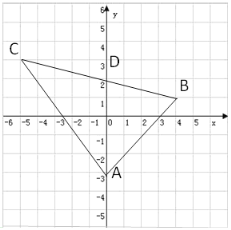
��1���ֵ�C�ڵ�A��ߺ͵�C�ڵ�A�ұ��������������⼴�ɵó��𰸣�
��2�������е㹫ʽ���㼴�ɵó��𰸣�
��3���ȸ����˶�������x����A�͵�B����ʾ��ֵ���ٷ���������������ۣ��ٵ�B��ԭ���ұߣ��ڵ�B��ԭ����ߣ��ֱ�������������OA��OB��ֵ������OA=2OB�г���ʽ���ⷽ�̼��ɵó���.
�⣺��1������C�ڵ�A����ߣ����C����ʾ����Ϊ��![]()
����C�ڵ�A���ұߣ����C����ʾ����Ϊ��![]()
�ʵ�C��ʾ����Ϊ-5��-11
��2�������֪����DΪAB�е�
���D��ʾ����Ϊ��![]()
��3��x����A��ʾ����Ϊ![]() ����B��ʾ����Ϊ
����B��ʾ����Ϊ![]()
�ٵ���B��ԭ���ұ�ʱ
OA=8+x��OB=12-2x
��OA=2OB
��8+x=2(12-2x)
��ã�![]()
�ڵ���B��ԭ�����ʱ
OA=8+x��OB=2x-12
��OA=2OB
��8+x=2(2x-12)
��ã�![]()
����������x��ֵΪ![]() ��
��![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�