题目内容
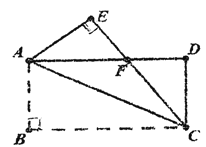
【题目】如图,AC是矩形ABCD的一条对角线,沿AC折叠使点B落在点E处。
(1)求证△AEF≌△CDF.
(2)若AB=4,BC=8,求△AEF的周长.
【答案】(1)详见解析;(2)12.
【解析】
(1)由矩形的性质可得AB=CD,AD=BC,∠B=∠D=90°,由折叠可知,AB=AE,∠B=∠E=90°,即可得∠E=∠D=90°,AE=CD,利用AAS即可证得△AEF≌△CDF;(2)由全等三角形的性质可得EF=DF,再由△AEF的周长=AF+EF+AE=AF+FD+AE=AD+AE=BC+AB即可求解.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠B=∠D=90°,
由折叠可知,AB=AE,∠B=∠E=90°,
∴∠E=∠D=90°,AE=CD,
在△AEF和△CDF中,

∴△AEF≌△CDF;
(2)∵△AEF≌△CDF,
∴EF=DF,
∴△AEF的周长=AF+EF+AE=AF+FD+AE=AD+AE=BC+AB=8+4=12.

练习册系列答案
相关题目