题目内容
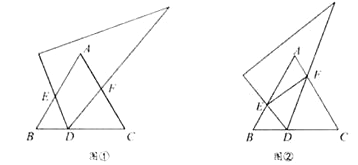
【题目】在数学课本中,有这样一道题:已知:如(图1),∠B+∠C=∠BEC求证:AB∥CD
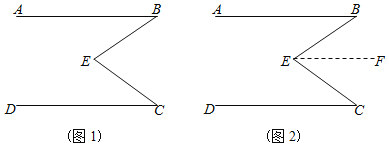
(1)请补充下面证明过程
证明:过点E,做EF∥AB,如(图2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)请再选用一种方法,加以证明
【答案】(1)BEF,C,FEC,CD;(2)见解析
【解析】
(1)利用平行线的判定和性质一一判断即可.
(2)如图1中,延长BE交CD于F,根据三角形的外角定理证明∠B=∠EFC即可.
(1)证明:过点E,做EF∥AB,如图2.
∴∠B=∠BEF,
∵∠B+∠C=∠BEC,∠BEF+∠FEC=∠BEC(已知),
∴∠B+∠C=∠BEF+∠FEC(等量代换),
∴∠C=∠FEC(等式性质),
∴EF∥CD,
∵EF∥AB,
∴AB∥CD(平行于同一条直线的两条直线互相平行)
故答案为:BEF,C,FEC,CD.
(2)如图1中,延长BE交CD于F.
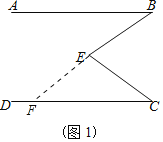
∵BEC=∠EFC+∠C,∠BEC=∠B+∠C,
∴∠B=∠EFC,
∴AB∥CD.

练习册系列答案
相关题目