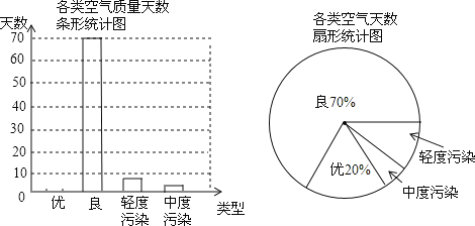
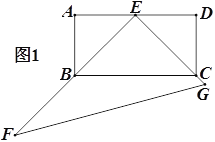
题目内容
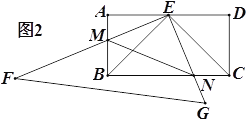
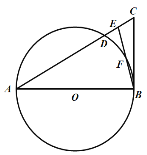
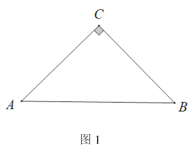
【题目】（1）如图1，△ABC 中，AC=BC，∠ACB=90°．请用直角三角尺（仅可画直角或直线）在图中画出一个点P，使得∠APB=45°；
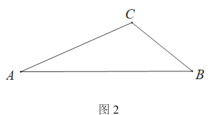
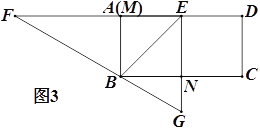
（2）如图2，△ABC 中，AB=a，∠ACB=
，请用直尺和圆规作出一个点Q，使点Q与点C在AB同侧，QA=QB，∠AQB=；（不写作法，保留作图痕迹）
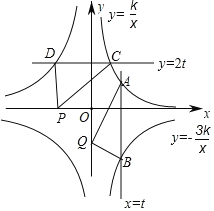
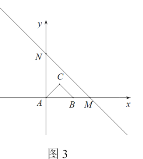
（3）如图3，若 AC=BC=
，∠ACB=90°，以点A为原点，直线AB 为 x 轴，过点A垂直于AB的直线为 y 轴，建立平面直角坐标系，直线y= - x+b(b>0)交 x 轴于点M，交 y 轴于点N．当点P在直线MN上，且∠APB=45°，求点P的个数及对应的b的取值范围；
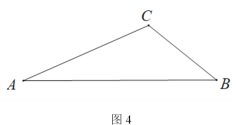
（4）如图4，△ABC 中，AB=a，∠ACB=，请用直尺和圆规作出点P，使得∠APB=且AP+BP最大，请简要说明理由．（不写作法，保留作图痕迹）
【答案】（1）见解析；（2）见解析；（3）当
时，点P的个数为2个，当
或
时，点P的个数为1个，当
时，点P有0个；（4）图见解析，理由见解析
【解析】
（1）画∠ABM=90°，延长AC与BM交于点P，则∠APB=45°；
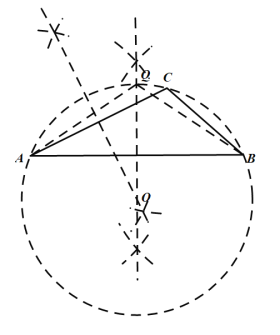
（2）作△ACB的外接圆与AB的垂直平分线交于点Q,则AQ=BQ,∠AQB=∠ACB=
；
（3）以点C为圆心，AC长为半径画圆，当直线
恰好与圆相切时，此时处于临界点，求出此时b的值，然后通过对直线的平移即可确定b的取值范围，通过平移后直线与圆的交点的个数即可确定点P的个数；
（4）在问题（2）已作图像基础上，以点Q为圆心，AQ长为半径作圆，在
上取一点
即可满足
，然后延长
交⊙Q于点F，连接FB，易证
，
，当AF 为直径时最大，即点P为弧AB中点时最大．
解：(1)如图：
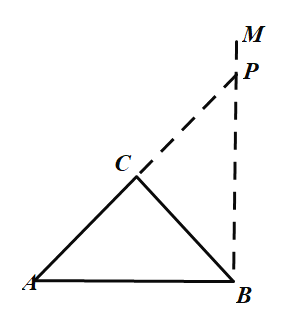
（2）如图：
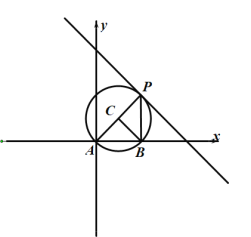
(3)如图，以点C为圆心，AC长为半径画圆，当直线恰好与圆相切时，设切点为P，此时
,
，
，
，
，
∴点P的坐标为
，
将点P代入中得，
解得 ．
当直线恰好平移到与BC重合时，点B在直线上，将点B（2，0）代入中得，
，解得
．
然后通过对直线的平移之后得到的新直线与圆的交点的个数即可得出P点的个数，
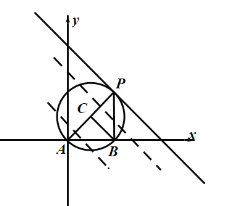
当时，不存在这样的P点，当时，存在两个P点，当
时，虽然直线与圆有两个交点，但是其中一个点不满足题意，所以只存在一个P点．
综上所述，当时，点P的个数为2个，当或 时，点P的个数为1个，当时，点P有0个，；
(4)如图，
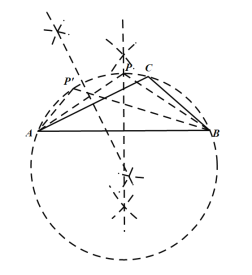
理由如下：
在问题（2）已作图像基础上，以点Q为圆心，AQ长为半径作圆，在 上取一点 即可满足 ，然后延长 交⊙Q于点F，连接FB，
,
当AF 为直径时最大，即点P为弧AB中点时最大
